Гамма на основе критерия хи-квадрат средствами Statistica.
Таблица 3.
|
Observed |
Cumulative Observed |
Percent Observed |
Cumul. % Observed |
Expected Frequency |
Cumulative Expected |
Percent Expected |
Cumul. % Expected |
Observed- Expected |
|
|
<= 11,111 |
51 |
51 |
25,62814 |
25,6281 |
51,87901 |
51,8790 |
26,06985 |
26,0699 |
-0,87901 |
|
22,222 |
63 |
114 |
31,65829 |
57,2864 |
65,13076 |
117,0098 |
32,72903 |
58,7989 |
-2,13076 |
|
33,333 |
45 |
159 |
22,61307 |
79,8995 |
41,30189 |
158,3117 |
20,75472 |
79,5536 |
3,69811 |
|
44,444 |
24 |
183 |
12,06030 |
91,9598 |
21,74218 |
180,0539 |
10,92572 |
90,4793 |
2,25782 |
|
55,555 |
11 |
194 |
5,52764 |
97,4874 |
10,47275 |
190,5266 |
5,26269 |
95,7420 |
0,52725 |
|
66,666 |
5 |
199 |
2,51256 |
100,0000 |
4,78789 |
195,3145 |
2,40597 |
98,1480 |
0,21211 |
|
77,777 |
0 |
199 |
0,00000 |
100,0000 |
2,11486 |
197,4294 |
1,06275 |
99,2107 |
-2,11486 |
|
88,888 |
1 |
200 |
0,50251 |
100,5025 |
0,91164 |
198,3410 |
0,45811 |
99,6688 |
0,08836 |
|
< Infinity |
0 |
200 |
0,00000 |
100,5025 |
0,65901 |
199,000 |
0,33116 |
100,000 |
-0,65901 |
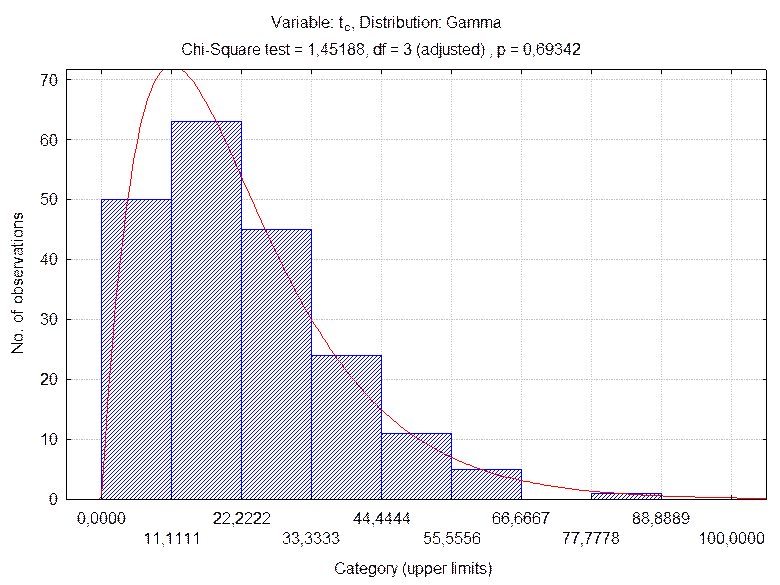 Рис. 3. Гистограмма распределения
времени нахождения заявки в системе
Рис. 3. Гистограмма распределения
времени нахождения заявки в системе
c наложением закона Гамма
Поскольку p-значение не меньше α (0,69342>0,05), гипотеза H0 призаданном уровне значимости не отвергается.
Среднее время пребывания требования в системе по результатам 10 экспериментов:
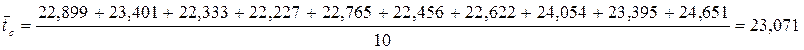 Среднее
время обработки одной заявки каналами результатам 10 экспериментов:
Среднее
время обработки одной заявки каналами результатам 10 экспериментов:
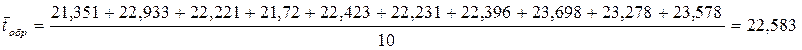 Среднее время ожидания в очереди
по результатам 10 экспериментов:
Среднее время ожидания в очереди
по результатам 10 экспериментов:
![]()
3.2. Имитация СМО с учетом дополнительных условий
По заданию одну заявку обслуживают два канала, значит, это система с взаимопомощью. Каждая заявка одновременно обслуживается двумя каналами, соответственно интенсивность обслуживания рассчитывается как суммарная интенсивность работы двух каналов.
Вероятность простоя системы:
![]()
Вероятность загрузки системы:
![]()
Вероятность загрузки 1 канала (без очереди):
![]()
Вероятность загрузки 1 канала (с очередью):
![]()
Вероятность отказа в обслуживании:
![]()
Среднее число требований в очереди:
![]()
Среднее число занятых каналов:
![]()
Среднее число заявок в системе:
![]()
Среднее время пребывания требования в системе:
![]()
Среднее время обработки одной заявки каналами:
![]()
Среднее время ожидания в очереди:
![]()
Увеличение интенсивности обслуживания заявок значительно сократило время их пребывания в СМО. Однако это не привело к улучшению характеристик системы. Среднее время ожидания в очереди увеличилось более чем в 3 раза (из-за ликвидации одного самостоятельного канала), а вероятность простоя системы – более чем в 1,2 раза (интенсивность потока поступления заявок намного меньше интенсивности потока их обработки). Поэтому можно сделать вывод, что в данной СМО взаимопомощь не является оптимальным решением задачи улучшения ее функционирования.
Таблица 4. Ошибки определения параметров СМО
|
Параметр |
Аналитический метод |
Метод ИМ |
Ошибка оценки показателя ε (в %) |
|
P0 |
0,6374 |
0,62 |
2,73 |
|
P1 |
0,2857 |
0,2974 |
4,1 |
|
P2 |
0,0727 |
0,0723 |
0,55 |
|
P3 |
0,0113 |
0,0109 |
3,54 |
|
Pзагр |
0,3626 |
0,38 |
4,8 |
|
n0 |
0,0113 |
0,0109 |
3,54 |
|
tож |
0,565 |
0,531 |
6,02 |
|
Nз |
0,4537 |
0,4631 |
2,07 |
|
J |
0,465 |
0,474 |
1,93 |
|
tc |
22,787 |
23,13 |
1,51 |
|
tобр |
22,222 |
22,552 |
1,49 |
Как видно из таблицы 4, оценки значений вероятностей и характеристик СМО, полученные в результате имитационного моделирования статистически близки с точными значениями, рассчитанными аналитически. Поэтому можно сделать вывод о довольно высокой эффективности имитационного метода применительно к решению данной задачи. Незначительные расхождения с аналитически рассчитанными значениями объясняются переходными процессами в системе, а также некачественной генерацией последовательностей случайных чисел.
Однако сама система, несмотря на маленькое время ожидания в очереди и низкую вероятность отказа в обслуживании, является довольно неэффективной: очень велика вероятность ее простоя.
Несколько улучшить характеристики заданной СМО может полная ликвидация одного из каналов обслуживания (однако при этом необходимо позаботиться об увеличении очереди до 3 - 4). В этом случае вероятность загрузки системы увеличится с 0,38 до 0,48, хотя остальные характеристики при этом несколько ухудшатся.
Примером реальной СМО может служить склад комплектующих для компьютера. Поскольку поток покупателей не очень значителен, довольно велика вероятность простоя, а образование очереди, наоборот, маловероятно. Это СМО полностью соответствует варианту без дополнительных условий. А варианту с дополнительными условиями соответствует ситуация, когда поступает большой заказ и все работники стараются как можно быстрее его выполнить (собрать все необходимые комплектующие, аксессуары и др.).
Выводы
По результатам проведенных исследований СМО можно сделать следующие
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.