Планирование экспериментов с имитационными моделями систем массового обслуживания (СМО) с использованием методов регрессионного анализа средствами системы моделирования GPSS/World и пакета Statistica

оптимальную структуру математической модели, а это в первую очередь влияет на точность с которой задача будет решена.

                        Другим недостатком метода является то, что для нелинейных моделей необходимо искать преобразования, которые позволяют свести задачу к «приблизительно линейной», при этом все получаемые оценки оказываются смещенными.

3.2.  Метод наименьших квадратов

Предположим, что между экспериментальными данными предполагается линейная зависимость:

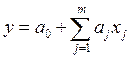                                 (2)

Зависимость (2) носит название линейной регрессии. Исходные данные для получения оценок параметров модели (2) обычно записывают в виде матриц:

           ,

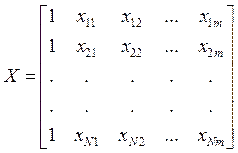
где i – номер эксперимента, N – их количество .

Для того, чтобы функция регрессии (2) достаточно хорошо описывала эмпирическую зависимость, ее параметры  подбирают таким образом, что отклонения  между измеренными  и теоретическими значениями 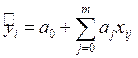 принимали бы минимальные значения. В качестве такого критерия выбирают сумму квадратов отклонений:

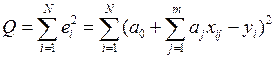                           (3)

Выбор критерия в таком виде объясняется тем, что при этом формулы расчета значений  достаточно просты, хорошо зарекомендовали себя в практике, а сами эти значения обладают определенными свойствами .Критерий (3) является обобщенным показателем рассеивания вокруг искомой линейной зависимости.

Параметры  подбирают из условий минимизации (3). Необходимым условием существования минимума критерия (3) является равенство нулю частных производных по неизвестным параметрам . Минимизируя функцию Q положим

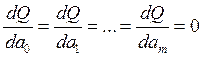                                          (4)

система линейных уравнений (4), как это легко найти, в матричной форме записывается

                                                             (5)

Из (5) следует, что

                                                     (6)

Оценку , найденную по формуле (6) называют оценкой наименьших квадратов, или оценкой МНК.

 3.3. Оценка точности и качества модели.

3.3.1 Проверка модели по величине остаточной дисперсии          

Принципиальная возможность применения модели, т.е. оценка адекватности полученной модели и изучаемого объекта, производится с помощью показателя остаточной дисперсии

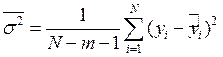                                                  (7)

Как доказано, например в [1,2],  является несмещенной и состоятельной оценкой дисперсии случайной составляющей, а величина 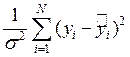 (если случайная величина нормальна) распределена по закону  с  степенями свободы.

3.3.2 Алгоритм проверки значимости выборочных коэффициентов регрессии

Известна [2] формула, позволяющая вычислить  - оценку дисперсии оценок :

                                              (8)

где  - диагональный элемент матрицы: . Соотношения (8) и утверждения, изложенные в пункте 3.3.1,  позволяют проверять гипотезы о значимости выборочных коэффициентов регрессии. Если расчетная значимость j – ого коэффициента

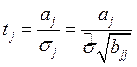                          (9)

меньше по модулю теоретической значимости , то теоретический коэффициент регрессии принимается равным нулю , с вероятностью ошибки . Здесь  - значение  - статистики Стьюдента с  доверительной вероятностью и  степенями свободы.

Известен алгоритм последовательного исключения факторов из модели. На каждом этапе рассчитываются эмпирические значимости всех коэффициентов регрессии  по формуле (9). Затем они ранжируются по назначению их модулей, и если минимальное значение оказывается меньше теоретической значимости, то соответствующий коэффициент выводится из модели и все расчеты повторяются. Расчеты заканчиваются тогда, когда все коэффициенты регрессии оказываются значимыми.

3.3.3 Критерий Фишера            
Оценкой качества всей модели в целом может служить критерий Фишера: если
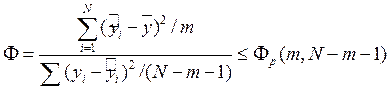                                            (10)
то уравнение в целом незначимо. Здесь  - критическая граница распределения Фишера  с  степенями свободы соответствующая уровню значимости  р;  - среднее значение . Вычисление отношения (10) позволяет выявить, насколько существенно различие этих двух показателей, т.е. в какой мере замена  на  улучшает наши представления о характере зависимости.
Применение Ф-критерия дает возможность конкретно оценить