3. Планы первого и второго порядка
3.1. Методические основы планирования эксперимента
При планировании эксперимента необходимо обеспечить получение достоверной информации для определения взаимосвязи между параметрами изучаемого объекта при минимальном количестве опытов. Этого можно достигнуть, следуя при планировании определенным правилам, учитывающим вероятностный характер результатов измерения и наличие внешних помех, воздействующих на изучаемый объект.
Результат измерения является достаточно достоверным только в случае его частой повторяемости при многократных измерениях. При воздействии на изучаемый объект, не изменяющийся при проведении опытов, помехи в результат измерения вносится систематическая ошибка. Такие ошибки могут быть устранены, если эксперимент спланирован так, что воздействие всех возможных помех станет случайным, т.е. при рандомизации эксперимента. Это достигается, например, выбором в случайной последовательности образцов металла из различных партий, проведением опытов в различное время суток, использованием в опытах различных машин и приборов.
Достоверность результата эксперимента повышается с увеличением числа опытов, но при этом возрастают материальные затраты и трудоемкость исследования. Статистически значимый результат должно обеспечивать минимальное число опытов. Статистические оценки точности измерений могут быть получены только после выполнения опытов. Поэтому оптимальной является стратегия последовательного эксперимента, при которой после каждого очередного опыта или серий опытов производится анализ результатов. Опыты прекращают при получении статистически значимого результата.
Количественную зависимость выходного параметра изучаемого объекта от входных параметров можно выразить, например, в виде
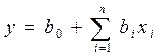 (3.1)
(3.1)
где y –выходной параметр; хi- входные параметры.
По опытным данным нужно определить коэффициенты bi. Эту задачу можно решить различными методами, например, варьируя каждый входной параметр по очереди. Если для определения каждого коэффициента bi сделано n повторных опытов и если параметры изменены только на двух уровнях, то Дисперсия, оценивающая точность коэффициентов bi
![]() (3.2)
(3.2)
ее зависит от общего количества входных параметров, воздействие которых исследуется, а значения коэффициентов bi определяются всего двумя усредненными измерениями, задающими значение дисперсии коэффициента bi,
По другой методике все параметры можно варьировать совместно так, что оказывается возможным оценить воздействие каждого входного параметра на выгодной параметр объекта по всей совокупности опытов. В этом случае необходимо проделать m+1 опытов. Как и по ранее рассмотренной методике, такая серия опытов может быть повторена
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.