Механические и физические свойства материалов: Методические указания к выполнению курсовой работы, страница 3

Номинальная контактная удельная нагрузка для пары трения типа подшипника скольжения определяется

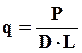
3. РАССЧЕТ ДИФФУЗИОННЫХ ПРОЦЕССОВ

Теоретический анализ диффузионных процессов базируется на решении дифференциального уравнения

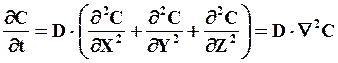                                                     (18)

Учитывая, что ширина диффузионной зоны значительно на несколько порядков меньше диаметрального размера самой зоны решение уравнения (18) приводится к одномерной задаче. Поверхность, через которую осуществляется диффузионный массоперенос, представляют в виде прямой плоскости, при этом массовый поток направляется в глубь полубесконечного тела (рис.9). В линейном варианте температура процесса и коэффициент диффузии постоянны во времени. Решение дифференциального уравнения сводится к нахождению закона изменения концентрации диффундирующего элемента по глубине полубесконечного тела в зависимости от времени процесса С(Х, t).

Итак, в одномерном варианте уравнение Фика второго рода представляется в виде

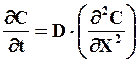                                                               (19)

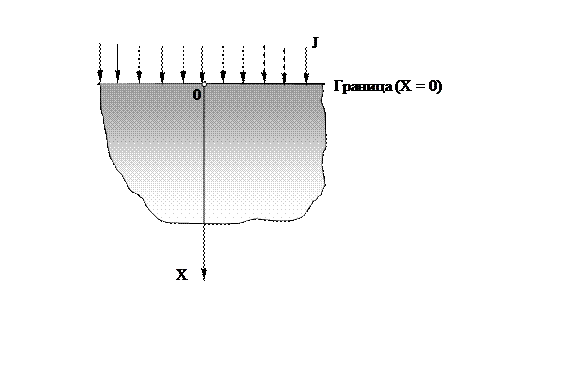
Рис. 9. Одномерная диффузионная модель

Рассмотрим основные варианты решения диффузионных задач.

1. Диффузия в полубесконечный образец с нулевой начальной концентрацией диффузанта С(Х, 0) = 0 из другого полу ограниченного образца с начальной концентрацией С₀. Решение принимает следующий вид

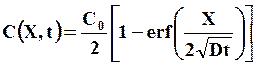                                             (20)

Концентрационные кривые представлены на рис. 10.

2. Диффузия в образец с нулевой начальной концентрацией через поверхность (Х = 0), на которой поддерживается постоянная концентрация С₀, не зависящая от времени, т.е. С(0,t) = C₀. закон распределения концентрации диффундирующего элемента описывается выражением

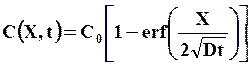
                                            (21)

Обратной этой задаче является вариант диффузии из полуограниченного образца с начальной концентрацией С₀ через поверхность (Х = 0) в среду, не содержащего диффундирующего вещества, т.е. на поверхности всегда поддерживается нулевая концентрация С(0,t) = 0. Решение принимает следующий вид

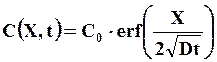                                                       (22)

Рис. 10. Концентрационные кривые для полубесконечных образцов:

а – состояние образцов до нагрева; б – состояние образцов после нагрева;

с – кривая распределения концентрации диффузанта (t₁ < t₂ < t₃).

3. Диффузия из образца с заданной начальной концентрацией С₀ через поверхность (Х =0), на которой массообмен происходит по закону

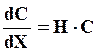                                                                               (23)

где Н – const.

Решение принимает вид

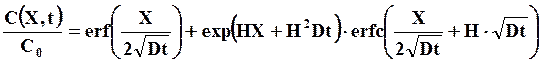                   (24)

На самой поверхности (Х = 0)концентрация меняется по закону

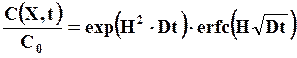                                                          (25)

Обратная задача – диффузия из среды с постоянной концентрацией в полуограниченное тело с нулевой концентрацией при граничных условиях (23). Решение представляет следующее выражение

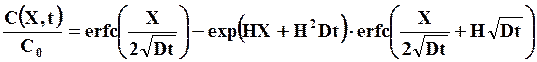           (26)

Количество вещества, прошедшее через единичную площадь поверхности за время t можно определить как

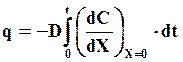                                                                      (27)