Температурный интервал, в котором справедлива формула (4.18), для реальных металлов не большой в среднем в диапазоне от 0 до 4оК. При плавлении также наблюдается отклонение электросопротивления от линейной зависимости. В большинстве случаев имеет место резкое увеличение сопротивления, реже наблюдается его уменьшение (рис. 4.2).
Рис. 4.2. Температурная зависимость удельного электрического
сопротивления металлов
4.3. Электросопротивление металлов при наличии примесей
Причинами рассеивания электронных волн могут быть примесные атомы и искажения решетки, вызванные различными видами обработки. Согласно правилу Маттиссена, коэффициент рассеивания в этом случае должен содержать столько слагаемых, сколько причин вызывают рассеивание электронной волны. Если рассеивание происходит только вследствие нагревания проводника и наличия примесей, то коэффициент рассеивания содержит два слагаемых, из которых один – тепловой, характеризующийся средней длиной свободного пробега lт, а второй – характеризующий рассеивание электронов на примесных атомах со средней длиной пробега lп. Тогда общее электросопротивление проводника будет
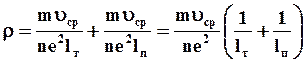(4.19)
где первое слагаемое связано с тепловым рассеиванием электронной волны, а второе – за счет примесных атомов.
Исследование электросопротивления в зависимости от содержания примесей показывает, что любое количество введенной в чистый металл примеси приводит к повышению его сопротивления, даже если примесная добавка обладает повышенной электропроводностью по сравнению с основным металлом.
Электросопротивление в твердых растворах, особенно неупорядоченных, в которых имеются два и более сорта атомов, распределенных относительно беспорядочно в атомно-кристаллической структуре, оказывается во много раз большим, чем в исходных чистых компонентах. Это объясняется тем, что различие электрических зарядов и размеров атомов, составляющих раствор, приводит к нарушению периодичности поля решетки, к искажению кристаллического строения в местах нахождения разносортных атомов. В непрерывном ряду твердых растворов электросопротивление тем больше, чем дальше по своему составу сплав отстоит от чистых исходных компонентов. Максимальное сопротивление в двойных сплавах, как правило, регистрируется при 50% атомарной концентрации, причем оно может в несколько раз превышать сопротивление чистых металлов. Сопротивление твердых растворов можно описать обобщенной формулой
(4.20)
где с – атомная концентрация одного из компонентов.
Если при изменении концентрации компонентов, при определенном их соотношении, образуется упорядоченный твердый раствор, то электросопротивление в этой области падает.
При нагревании твердых растворов темп роста их сопротивления значительно ниже, чем у чистых металлов. Вследствие этого температурный коэффициент (α) у твердых растворов всегда меньше, чем у исходных компонентов, и меняется в зависимости от состава аналогично проводимости.
При образовании химических соединений электрическое сопротивление увеличивается более резко, чем при образовании твердых растворов. Это объясняется тем, что при образовании химических соединений металлическая связь между атомами заменяется на ковалентную, в результате чего концентрация носителей тока – коллективизированных электронов уменьшается. Подобные изменения характера межатомных связей при химическом взаимодействии приводят к тому, что получаемые соединения часто оказываются полупроводниками.
Если при сплавлении двух и более компонентов образуются механические смеси чистых компонентов или смеси чистых компонентов с их твердыми растворами, химическими соединениями и т.д., то электрическое сопротивление сплава, состоящего из нескольких фаз, определяется проводимостью этих фаз. Для расчета электросопротивления необходимо знать проводимость и объемное содержание каждой фазы. В том случае, когда одна из фаз образует непрерывно связанную матричную основу, в которую вкраплены несоприкасающиеся между собой кристаллы второй фазы, то электропроводность сплава при любом соотношении фаз определится формулой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.