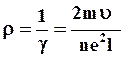Электрические свойства материала. Теория электропроводности металлов. Электросопротивление металлов при наличии примесей. Электрические свойства неметаллов, страница 2

                                                                                     (4.12)

С учетом (4.9)  окончательно получим

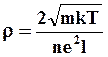                                                                                        (4.13)

Из (4.13) следует, что согласно классической теории удельное электрическое сопротивление прямо пропорционально квадратному корню от температуры и обратно пропорционально длине пробега электрона между столкновениями.

Классическая теория электропроводности хорошо объясняет оптические свойства металлов, но не раскрывает физический смысл длины свободного пробега электрона и входит в противоречие с целым рядом экспериментальных результатов, в частности, не объясняет линейное изменение электросопротивления с повышением температуры. Это противоречие снимается теорией электрического сопротивления, обусловленного  рассеиванием электронной волны на тепловых колебаниях решетки.

Согласно квантовой теории перенос электричества в металле связан с распространением электронной волны, в формировании которой участвуют только те электроны, энергия которых превышает энергию Ферми. Электрическое сопротивление определяется рассеиванием электронной волны на различных искажениях решетки и неоднородностей распределения плотности рассеивающих центров, которые вызываются тепловыми движениями ионов, механическими деформациями и примесными атомами. Рассеивание электронной волны происходит, если расстояние между рассеивающими центрами по величине будут соизмеримо с ее длиной волны. Если расстояние между рассеивающими центрами значительно меньше длины волны, то рассеивание не будет и электронная волна в такой среде пройдет беспрепятственно.

В идеальном кристалле рассеивание обусловлено только нарушениями плотности распределения атомов из-за теплового колебания. При нагревании металла вследствие беспорядочных колебаний атомов будет происходить нарушение периодичности атомной плотности в кристалле, т.е. будут появляться места с малой и высокой атомной плотностью по сравнению с ее средним значением. Подобные отступления плотности от среднего значения представляют собой флуктуации по плотности. При низких температурах амплитуда тепловых колебаний атомов мала, что и определяет малое рассеивание и низкое сопротивление. С ростом температуры увеличивается амплитуда и разупорядочение в плотности, а также начинают проявляться флуктуации электрического поля решетки. Все это приводит к увеличению рассеивания, уменьшению длины свободного пробега электронов и повышению сопротивления.

Отклонение от положения равновесия при нагревании определяется амплитудой тепловых колебаний, квадрат которой прямо пропорционален температуре тела. Если предположить, что рассеивание электронных волн происходит не самими атомами, а теми сферами, которые описываются центром атома при тепловых колебаниях, то коэффициент рассеивания можно представит выражением

                                                                             (4.14)

где ε – амплитуда тепловых колебаний.

Амплитуда тепловых колебаний описывается выражением

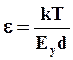                                                                                         (4.15)

где Е_у – модуль упругости решетки; d  - межплоскостное расстояние.

Тогда коэффициент рассеивания примет вид

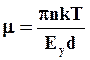                                                                                        (4.16)

Если в выражении (4.12) подставить вместо длины свободного пробега обратную величину коэффициента рассеивания, то удельное электросопротивление будет иметь следующий вид

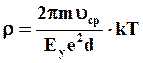                                                                              (4.17)

Формула (4.17) хорошо согласуется с экспериментальными данными. Отклонение электросопротивления от линейной температурной зависимости происходит  только при очень низких температурах и температуре плавления. Электрическое сопротивление многих металлов при низких температурах может быть найдено с помощью следующей формулы

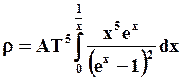                                                                (4.18)

где x = θ_Д/Т; θ_Д – температура Дебая; А – коэффициент, характеризующий металл.