Акустическая эмиссия. Изучение акустического излучения металлами при механической деформации, страница 4

Первые корреляционные зависимости были установлены в процессе прочностных испытаний материалов с одновременной регистрацией АЭ - информации. Из анализа многочисленных литературных источников можно сформулировать некоторые традиционные утверждения, позволяющие качественно оценить процесс накопления повреждаемости в материале и развитие разрушения.

1)  Суммарный счёт несёт информацию об интегральной повреждаемости объекта в процессе какого-либо внешнего воздействия, об увеличении длины дефекта и изменении его площади. В ранних работах, посвящённых методу АЭ, отмечается, что суммарный счёт взаимосвязан с амплитудой и длительностью импульсов АЭ, а, следовательно, и с энергией процесса разрушения. Это было актуально, когда используемая аппаратура не позволяла непосредственно измерять такие параметры, как длительность и энергия импульсов АЭ.

Характерная зависимость суммарного счёта от статической нагрузки показана на рисунке 1.4, a. По виду нарастающей зависимости суммарного счёта от возрастающего внешнего параметра, например давления, можно судить о степени активности источников АЭ и определить момент начала критического разрушения объекта (рисунок 1.4, б).

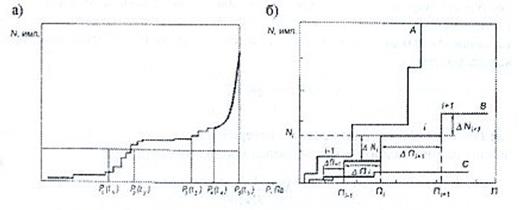
а – характерная зависимость числа импульсов АЭ от статической нагрузки; б – классификация активности источников АЭ по темпу нарастания суммарного счёта

Рисунок 1.4 – Зависимость суммарного счёта

Кривая С характеризует слабоактивный дефект и не требует внимания со стороны наблюдателей.

Кривая В характеризует активный дефект и требует постоянного внимания со стороны персонала, обслуживающего исследуемый объект.

Кривая А характеризует критически активный дефект, который может развиваться с большой скоростью. Необходима срочная остановка нагружения или эксплуатации объекта и его анализ различными методами неразрущающего контроля.

Начало опасной активности источников АЭ определяется моментом, когда показатель степени а зависимости , аппроксимирующей кривые нарастания суммарного счёта, равен четырём и более.

Современные методы оценки способности материалов сопротивляться развитию трещин сводятся, в основном, к определению критериев, характеризующих переход разрушения к закритической стадии. В качестве критерия сопротивления хрупкому разрушению в теории прочности используют коэффициент интенсивности напряжений . Коэффициент  характеризует способность материала сопротивляться развитию трещины в условиях плоской деформации.

Используя гипотезу, что суммарный счёт пропорционален объёму материала, вовлечённого в пластическую деформацию, и зависит от размера зоны, в которой происходит рост и слияние микротрещин, были получены соотношения связи суммарного счёта  с параметрами деформации  и разрушения материалов. Ниже представлены некоторые из этих зависимостей.

                                              ,

где     - суммарный счёт;

 - константа, зависящая от физико-механических свойств материала и чувствительности аппаратуры;

 - коэффициент интенсивности напряжений;

 - изменяется от 4,6 до 11, 9 в зависимости от класса материала.

                            ,

где      - постоянная, зависящая от материала и геометрии образца;

 - половина длины трещины;

 - предел прочности материала.

                                                  ,

где      - модуль упругости материала;

 – коэффициент интенсивности напряжений.

                                    ,

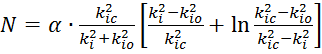где      – коэффициент пропорциональности;

 - критическое значение коэффициента интенсивности напряжений ;

 - начальное значение .

2)  Скорость счёта , как производная от суммарного счёта, отражает скорость развития повреждения материала в данный момент времени. Этот параметр обычно регистрирует совместно с суммарным счётом, и они дополняют друг друга в процессе анализа результатов эксперимента.

3)  Пиковая амплитуда , отдельных импульсов АЭ, а также энергия единичных сигналов  являются энергетическими показателями процесса повреждаемости материала. Если в эксперименте число акустических сигналов с определёнными параметрами равно числу образовавшихся микротрещин, то энергия сигнала будет пропорциональна размерам образующихся под нагрузкой трещин. Под напряжением  трещина диаметром  разрушает упругий объём .