![]() – постоянные времени, зависящие от
акустических свойств среды, в которой возник источник.
– постоянные времени, зависящие от
акустических свойств среды, в которой возник источник.
Возникает релаксационный тип сигнала АЭ.
Как для акселерационного, так и для релаксационного процессов предполагается, что в момент перехода начинает действовать источник напряжения ступенчатой формы,
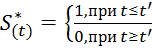 ,
,
где
![]() - момент времени перехода.
- момент времени перехода.
Полный сигнал
выражается произведением ![]() .
.
В результате анализа дислокационных механизмов возникновения источников АЭ можно сделать вывод, что основными формами сигналов АЭ являются видеоимпульсы релаксационного и акселерационного типа, которые описываются выражениями:
o для релаксационного сигнала:
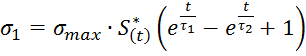 ;
;
o акселерационного сигнала:
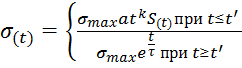 ,
,
где ![]() -
множитель, обеспечивающий необходимую размерность;
-
множитель, обеспечивающий необходимую размерность;
![]() -
коэффициент, определяемый физическим процессом, при излучении упругих волн.
-
коэффициент, определяемый физическим процессом, при излучении упругих волн.
Вид двух типов сигналов АЭ, представлен на рисунке 1.1.
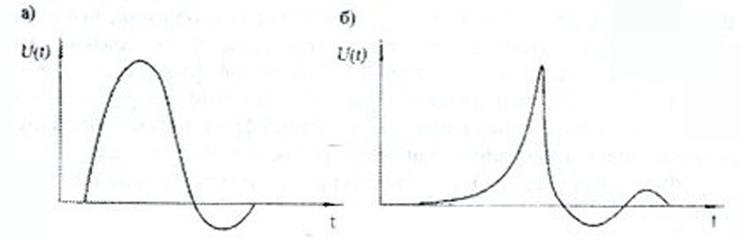
а – реласакционный; б - акселерационный
Рисунок 1.1 – Типы сигналов АЭ
Описанные механизмы и модели первичных (элементарных) сигналов в совокупности формируют полный сигнал АЭ. Учитывая, что АЭ является стохастическим импульсным процессом, полный сигнал является последовательностью импульсов релаксационного и акселерационного типов.
Третий вариант соответствует процессам излучения АЭ при развитии хрупкого разрушения. В работе рассмотрена модель формирования излучения АЭ на основе представления о разрыве атомных связей. В рассмотренной модели каждый элементарный импульс АЭ обусловлен релаксацией в результате разрыва единичной атомной связи, а полный сигнал излучения формируется из потока элементарных акустических импульсов.
При когерентном сложении элементарных импульсов и учёте «дифференцирующего» действия среды в работе было получено выражение вида
![]() ,
,
где
![]() – параметр решётки;
– параметр решётки;
![]() - постоянная затухания потока
акустических импульсов, связанная с размерами поля неоднородности.
- постоянная затухания потока
акустических импульсов, связанная с размерами поля неоднородности.
Форма импульса приведена на рисунке 1.2.

Рисунок 1.2 – Форма сигнала АЭ при хрупком разрушении материала
Машинное
моделирование процесса излучения упругой волны развивающейся трещиной в виде
эллипса с осями ![]() и
и ![]() (
(![]() – длина трещины) при условии, что
вся выделенная энергия при образовании новых поверхностей переходит в энергию
упругих волн, без учёта направленности излучения и диссипации энергии,
показывают, что импульс разгрузки однополярен и имеет форму купола или пика.
– длина трещины) при условии, что
вся выделенная энергия при образовании новых поверхностей переходит в энергию
упругих волн, без учёта направленности излучения и диссипации энергии,
показывают, что импульс разгрузки однополярен и имеет форму купола или пика.
Импульс
разгрузки при образовании и росте трещины ![]() мм с
постоянной скоростью, равной
мм с
постоянной скоростью, равной ![]() (
(![]() - скорость
роста трещины,
- скорость
роста трещины, ![]() - скорость
звука в материале), показан на рисунке 1.3.
- скорость
звука в материале), показан на рисунке 1.3.
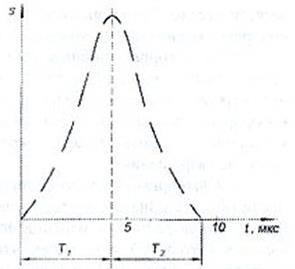
![]() – длительность переднего фронта;
– длительность переднего фронта; ![]() - длительность заднего фронта
- длительность заднего фронта
Рисунок 1.3 – Импульс разгрузки при образовании трещины
Если скорость роста трещины не остается постоянной, то на фронтах импульса разгрузки появляются перегибы. Увеличение скорости роста трещины приводит к перегибу на переднем фронте импульса разгрузки, а ее снижение - к появлению перегиба на заднем фронте.
При построении модели трещины, как излучателя
упругих волн, для мгновенно образующейся трещины нормального отрыва и
поперечного сдвига постоянной длины ![]() ,
в работе сделан вывод, что длительность переднего фронта импульса АЭ совпадает
с временем раскрытия трещины. Оно определяется по формулам:
,
в работе сделан вывод, что длительность переднего фронта импульса АЭ совпадает
с временем раскрытия трещины. Оно определяется по формулам:
·
для внутренней трещины нормального отрыва ![]() ;
;
·
для трещины нормального сдвига ![]() ,
где
,
где ![]() -
скорость продольных волн в материале.
-
скорость продольных волн в материале.
В работе отмечается, что длительность заднего
фронта пропорциональна области релаксации, т.е. ![]() ,
где
,
где ![]() - параметр области
разгрузки материала.
- параметр области
разгрузки материала.
1.3 Сопоставление параметров трещинообразования с параметрами акустической эмиссии
С точки зрения использования метода АЭ в решении проблем физики прочности, неразрушающего контроля и прогнозирования несущей способности конструкций, представляется важным установление корреляционных связей между параметрами АЭ и конкретными процессами, в результате которых происходит излучение самих упругих импульсов. Традиционный подход к решению данной проблемы заключается в использовании эталонных образцов и установлении, в большинстве случаев, качественных зависимостей между каким-либо параметром АЭ и конкретным физическим процессом в исследуемом материале.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.