Решение системы линейных уравнений

этом будем считать, что базисный минор (ненулевой минор максимального по-

рядка) основной матрицы находится в верхнем левом углу, то есть в него входят только

коэффициенты при переменных

.

Тогда переменные

называются главными переменными. Все остальные на-

зываются свободными.

Если хотя бы одно число

, где

, то рассматриваемая система несовместна.

Пусть

для любых

. Перенесѐм свободные переменные за знаки равенств и

поделим каждое из уравнений системы на свой коэффициент при самом левом (

, где — номер строки):

Где

.

Если свободным переменным системы (2) придавать все возможные значения и ре-

шать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего

уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система по-

лучена путѐм элементарных преобразований над исходной системой (1), то по теореме об

эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то

есть множества их решений совпадают.

3

1.1.3. Реализация метода в MathCAD

В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref(A).

Далее показано решение системы линейных уравнений методом Гаусса, в котором

используются следующие функции:

rref(A) - возвращается ступенчатая форма матрицы А.

augment(A, В) - возвращается массив, сформированный расположением A и В бок о

бок. Массивы A и В должны иметь одинаковое число строк.

submatrix(A, ir, jr, ic, jc) - возвращается субматрица, состоящая из всех элементов

с ir по jr и столбцах с ic по jc.

Дана система уравнений:

Матрица системы:

Матрица правой части:

1 23

6

a

23

4

b

20

325

6

Чтобы столбцы и строки матрицы нумеровались, начиная с единицы, присвоим

переменной ORIGIN значение, равное единице.

ORIGIN

1

Определитель матрицы:

a

58

Формирование расширенной матрицы системы:

ab

augment ( a b)

1

23

6

ab

23

4 20

3

2

56

Приведение расширенной матрицы к ступенчатому виду:

ag

rref ( ab)

1008

ag

0104

0012

Формирование столбца решения системы:

x

submatrix( ag 1 3 4 4)

8

x

4

2

Получили решение системы: x1=8, x2=4, x3=2.

4

1.1.4. Проверка правильности решения системы уравнений

Дана система уравнений (вариант 9):

Решить данную систему уравнений методом Гаусса.

Запишем расширенную матрицу системы:

Далее требуется сделать эквивалентные преобразования и привести матрицу к тре-

угольному виду:

Определитель системы уравнений равен -58, значит система имеет решение:

Далее подставим

во второе уравнение:

Полученные

подставим в первое уравнение:

Итоговое решение системы выглядит следующим образом:

что соответствует полученному выше при использовании средств MathCAD.

5

1.2. Решение системы линейных уравнений средствами мат-

ричного исчисления

1.2.1. Задание (вариант 9)

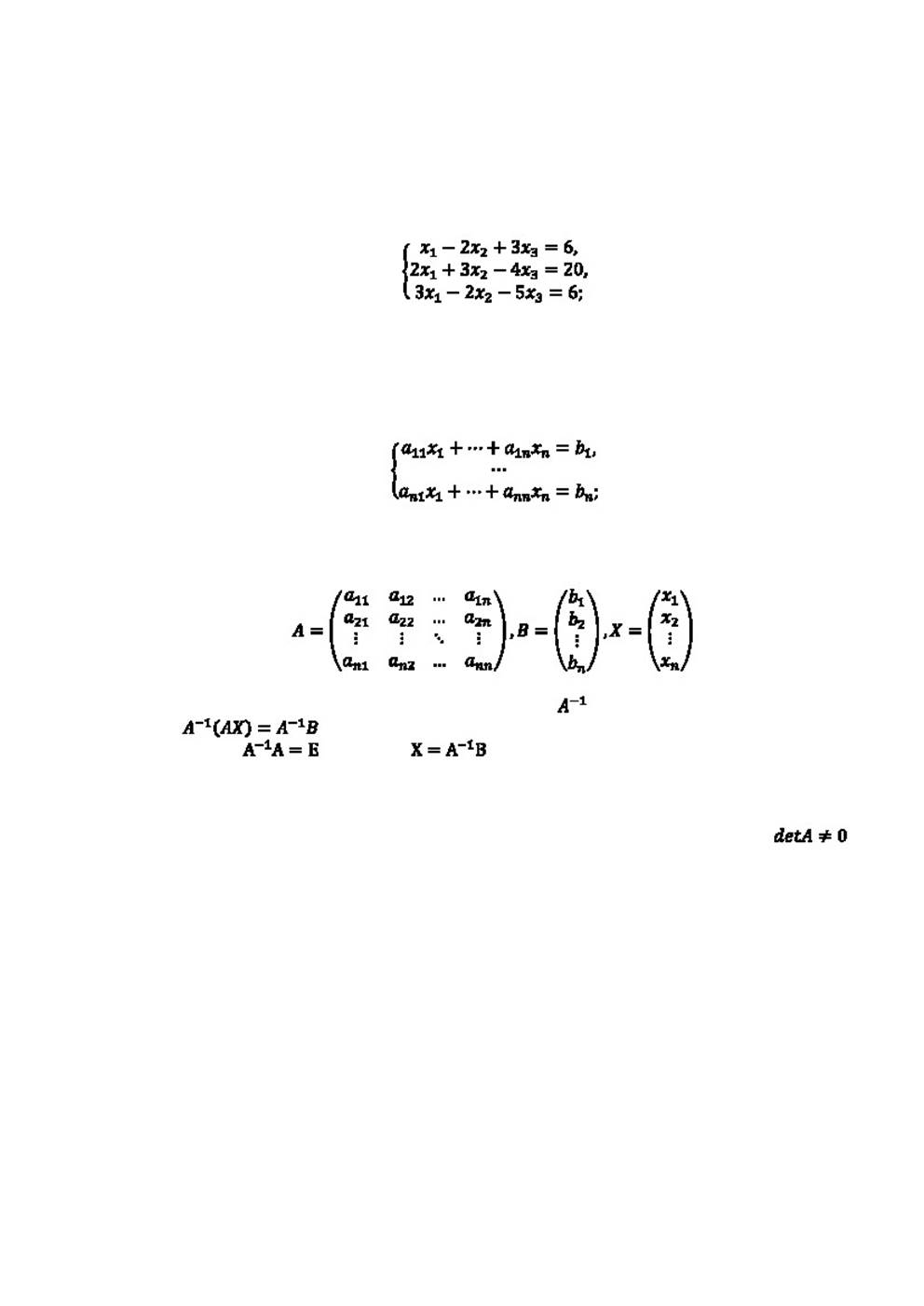
Доказать совместность системы уравнений и решить еѐ средствами матричного ис-

числения:

1.2.2. Описание метода

Матричный метод решения систем линейных алгебраических уравнений с ненуле-

вым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным по-

лем):

Тогда еѐ можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и

решений системы соответственно:

Умножим это матричное уравнение слева на

— матрицу, обратную к матри-

це A:

.

Так как

, получаем

. Правая часть этого уравнения даст столбец

решений исходной системы. Условием применимости данного метода (как и вообще су-

ществования решения неоднородной системы линейных уравнений с числом уравнений,

равным числу неизвестных) является невырожденность матрицы A. Необходимым и дос-

таточным условием этого является неравенство нулю определителя матрицы A:

.

6

1.2.3. Реализация метода в MathCAD

Требуется решить систему линейных уравнений методом матричного исчисления.

Решим данную систему при помощи матричного метода.

Запишем главный определитель системы (матрицы) и убедимся в том, что определи-

тель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

1 23

a

23

4

325

58 - определитель отличен от нуля, система имеет решение.

a

Далее находим обратную матрицу:

0.397 0.276 0.017

1

a

0.034 0.241

0.172

0.224 0.069 0.121

Для получения матрицы решений перемножим обратную матрицу и столбец свобод-

ных членов.

6

8

1

x

a

20

4

6

2

Получили решение системы уравнений:

x1 8 ; x2 4 ; x3

2.

7

1.2.4. Проверка правильности решения системы уравнений

Дана система уравнений (вариант 9):

Решить данную систему уравнений методом матричного исчисления.

Запишем матрицу системы, найдѐм определитель, и убедимся в том, что определи-

тель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю