

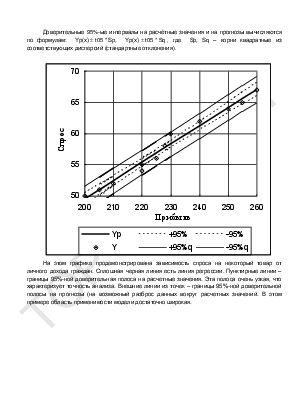
Регрессионный анализ является основным математическим инструментом для анализа зависимостей в эконометрии. Однако этот анализ не должен завершаться только оценкой параметров математической модели. Необходимо еще рассчитать и построить графики зависимостей вместе с 95%-ными доверительными интервалами на каждое расчетное значение (Confidence Limits) и на прогнозы, учитывающие возможный разброс точек вокруг линии регрессии (Prediction Limits). Только наличие на графиках этих доверительных полос дает возможность установить пределы применимости регрессионной модели. Модель применима только в той области варьирования факторов, в которой доверительная полоса относительно узкая и гарантирует достаточную точность прогнозов. Расчеты доверительных интервалов в многомерном случае исключительно сложны, требует применения матричного аппарата и программного обеспечения на компьютере, которое способно непосредственно оперировать с матрицами. Универсальная электронная таблица Excel обладает такими возможностями, она имеет целый ряд функций диапазонов, к которым, в частности, относятся функции матричной алгебры – умножения, транспонирования и обращения матриц. Существуют также специализированные статистические системы, в которых предусмотрено выполнение этих же расчетов в автоматическом режиме, но здесь сразу же надо иметь в виду, что все эти программные средства являются лицензионными продуктами, и использование их без заключения лицензионного соглашения не законно. В то же время электронная таблица Excel, входящая в стандартный набор программ Microsoft Office, является вполне легальным продуктом, установленном практически на каждом персональном компьютере.
На языке матричной алгебры вид многих формул становится достаточно простым. До недавнего времени (напоминаем, что персональные компьютеры появились всего 20 лет назад) это была обманчивая простота, т.к. для вычислений все-равно надо было переходить назад к координатной форме, и требовалось очень много вычислений там, где запись выражения в матричной форме размещалась в одной строке. Но теперь имеется возможность не только выводить матричные формулы, но также получать результаты, не особо интересуясь, сколько для этого компьютер выполнил арифметических операций.
Приведем необходимые матричные формулы регрессионного анализа.
Линейная многомерная модель имеет вид:
y = b0 + b1×x1 + b2×x2 + b3×x3 + ...+ bm×xm + e
где b0 , b1 , b2 , b3 , ... bm×– параметры модели, которые следует определить;
e – ошибки (остатки модели).
Для определения параметров модели ("оценки параметров") имеется ряд наблюдений, которые можно записать в виде матриц-столбцов:
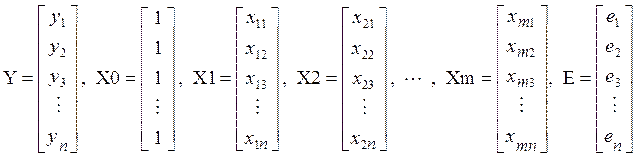
Здесь неизвестные пока ошибки для каждого наблюдения записаны также в виде матрицы-столбца. Для удобства введен единичный столбец Х0.
Тогда линейную модель для всех наблюдений можно записать в виде:
Y = b0*X0 + b1*X1 + b2*X2 + … + bm*Xm + Е,
или, в матричной форме если ввести матрицу Х = [X0, X1, X2, … , Xm] и вектор параметров модели (коэффициентов регрессии ВТ = (b0 , b1 , b2 , … , bm ):
Y = ХВ + Е .
Параметры модели определяем по методу наименьших квадратов (МНК), согласно которому вектор ошибок должен быть ортогонален к каждому члену модели, что в матричной форме записывается в виде XTE = 0.
Умножим матричное уравнение Y = ХВ + Е слева на ХТ и учтём, что ХТЕ = 0. Получим такую систему уравнений относительно параметров:
(ХТХ)В = ХТY.
Обозначим обратную матрицу этой системы через С = (ХТХ)–1 , тогда
В = С(ХТY).
Расчётные значения можно вычислить в виде матричного сумма
Yp = XB.
Переходим к выводу дисперсий расчетных значений.
Принимаем условия регрессионного анализа (Гауса - Маркова):
1) Y = Хb + e®модель линейная, случайные ошибки e относятся только к Y;
2) М(e) = 0 ®систематических ошибок не имеет;
3) М(eeT) = s2I ®наблюдения независимы М(eiej)=0 и равноточные М(ei2)=s2;
4) e~ N(0; s2I)®случайные ошибки наблюдений распределены нормально.
Из последнего условия вытекает, что наилучшей процедурой оценивания будет метод наименьших квадратов (МНК), относительно которого оценки b параметров bнужно вычислять по формуле:
b = (XTХ)–1(XTY) = C(XTY),
Преобразим: b = C(XTY) = b + C(XTe), откуда вытекает, что оценки параметров b являются случайными величинами с матожиданиями M(b) = b (т.е. оценки b – несмещенные) и ковариационной матрицею:
Sbb = M(b–b)(b–b)T = = M(CXTe)(CXTe)T = CXTM(eeT)XCT = s2C(XTX)CT = s2C.
Дисперсии коэффициентов регрессии оказались пропорциональными диагональным элементам обратной матрицы С.
Расчётные значения Yр = Ub = b0 + b1*x1 + b2*x2 + … + bm*xm являются линейными комбинациями случайных величин b с известной ковариационной матрицей. Так как дисперсия суммы равна сумме дисперсий плюс удвоенная ковариация, то Spp = M(Ub–Ub)(Ub–Ub)T = USbbUT = s2UCUT; несмещенную оценку дисперсии расчётных значений будем обозначать также Spp = MSE*UCUT. Тут С = (XTХ)–1 – обращёння матрица, U = (1, x1, x2, … , xm) – ряд значений объясняющих переменных. Для одномерной регрессией (m = 1) формула для Spp упрощается: Spp = (s2 /n) * (1 + (X–Xcp)2/ Sxx), де Sxx = ДИСПР(Х), s2 = MSE.
Наблюдения группируются около расчётных значений (линии регрессии), поэтому дисперсия прогнозных значений равняется: Sqq = Spp + MSE.
Доверительные 95%-ые интервалы на расчётные значения и на прогнозы вычисляются по формулам: Yр(х) ± t05 * Sp, Yр(х) ± t05 * Sq , где Sp, Sq – корни квадратные из соответствующих дисперсий (стандартные отклонения).
![]()
|
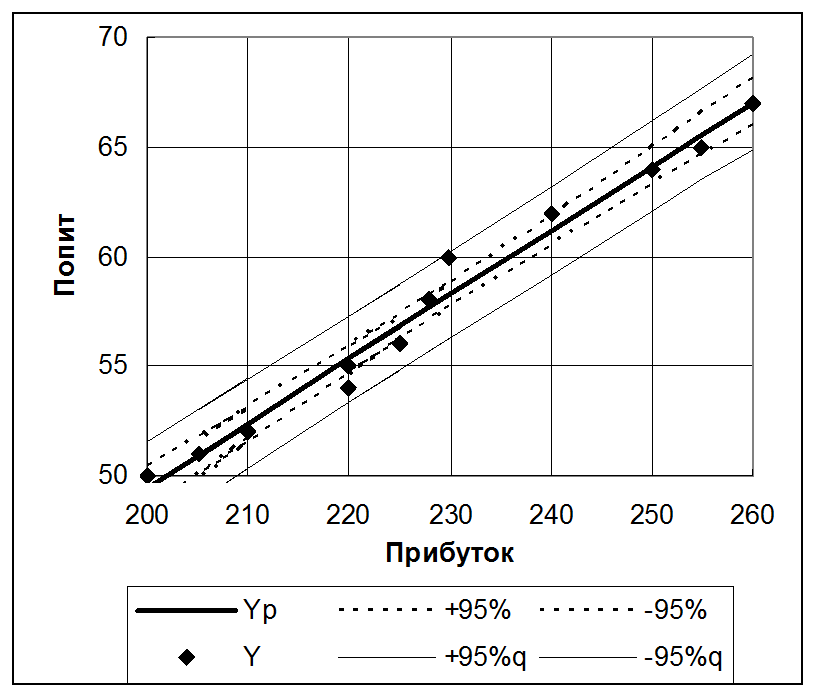
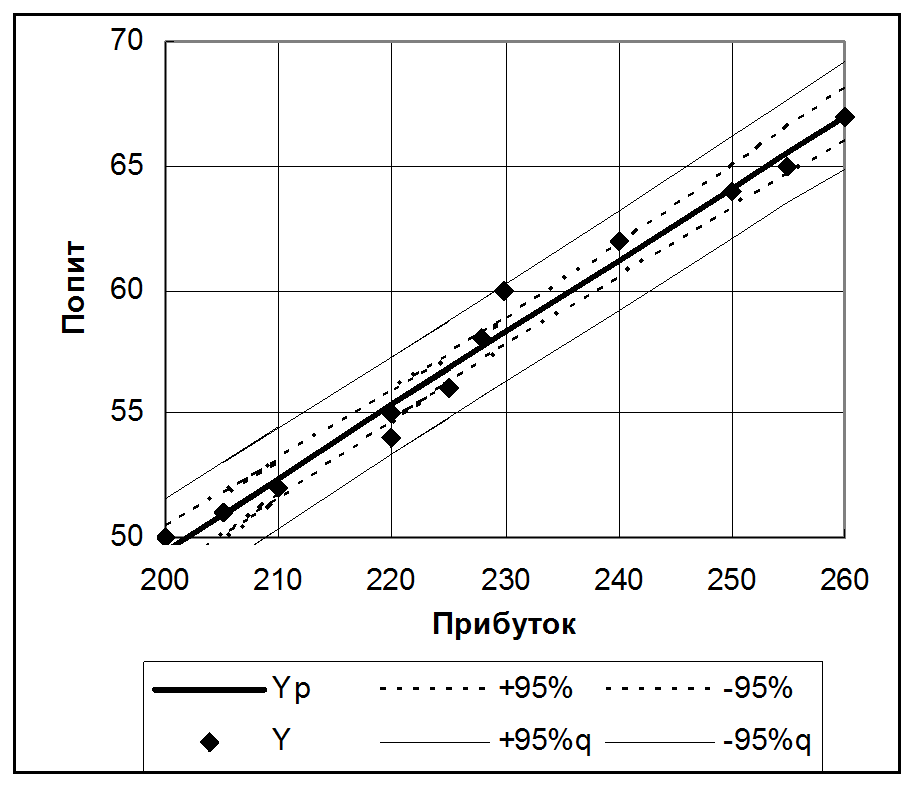
На этом графике продемонстрирована зависимость спроса на некоторый товар от личного дохода граждан. Сплошная черная линия есть линия регрессии. Пунктирные линии – границы 95%-ной доверительная полоса на расчетные значения. Эта полоса очень узкая, что характеризует точность анализа. Внешние линии из точек – границы 95%-ной доверительной полосы на прогнозы (на возможный разброс данных вокруг расчетных значений. В этом примере область применимости модели достаточно широкая.
![]()
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.