Множественная Регрессия - Y
Множественный Регрессионный анализ
-----------------------------------------------------------------------------
Зависимая переменная: Y
-----------------------------------------------------------------------------
Стандарт T
Ошибка Оценки(Сметы) Параметра Статистическое P-значение
-----------------------------------------------------------------------------
КОНСТАНТА 0,233652 0,108958 2,14442 0,0576
X1-0,075907 0,0371665-2,04235 0,0684
X3 0,509772 0,170866 2,98345 0,0137
-----------------------------------------------------------------------------
Дисперсионный анализ
-----------------------------------------------------------------------------
Исходная Сумма Квадратов(Площадей) Df Означает Квадратное P-значение F-отношения(F-коэффициента)
-----------------------------------------------------------------------------
Моделируйте 0,00382075 2 0,00191037 5,24 0,0278
Остаточный 0,00364648 10 0,000364648
-----------------------------------------------------------------------------
Общее количество (Поправка). 0,00746723 12
R-squared = 51,1669 процентов
R-squared (откорректированный для d.f.) = 41,4002 процента
Стандартная Ошибка Оценки. = 0,0190958
Средняя(Скупая) абсолютная погрешность = 0,0121101
Durbin-Уотсон, статистический = 2,30072 (P=0,2984)
Задержка 1 остаточная автокорреляция =-0,214158
Пошаговый регресс
-------------------
Метод: обратный(отсталый) выбор
F-to-enter: 4,0
F-to-remove: 4,0
Шаг 0:
---------
4 переменные в модели. 8 d.f. для ошибки.
R-squared = Откорректированные 65,09 % R-squared = 47,64 % MSE = 0,00032583
Шаг 1:
---------
Удаление переменной X2 с F-to-remove = 0,467446
3 переменные в модели. 9 d.f. для ошибки.
R-squared = Откорректированные 63,05 % R-squared = 50,74 % MSE = 0,00030655
Шаг 2:
---------
Удаление переменной X4 с F-to-remove = 2,89524
2 переменные в модели. 10 d.f. для ошибки.
R-squared = Откорректированные 51,17 % R-squared = 41,40 % MSE = 0,000364648
Конечная(Заключительная) выбранная модель.
StatAdvisor
---------------
Вывод показывает результатам приспособления линейному множителю
модель регресса, чтобы описать отношения между Y и 4
независимые переменные. Уравнение приспособленной модели
Y = 0,233652 - 0,075907*X1 + 0,509772*X3
Так как P-значение в ANOVA таблице - меньше чем 0.05, есть a
статистически существенные отношения между переменными в
95%-ый доверительный уровень.
R-Squared статистический указывает что модель как приспособлено
объясняет 51,1669 % изменчивости в Y. Откорректированный R-squared
статистический, который является более подходящим для того, чтобы сравнить модели с различным(wотличным)
числа(номера) независимых переменных, являются 41,4002 %. Стандартная ошибка
оценка(смета) показывает среднеквадратичному отклонению residuals, чтобы быть
0,0190958. Это значение может использоваться, чтобы создать пределы предсказания для
новые наблюдения, выбирая опцию Reports от текстового меню.
Средняя(Скупая) абсолютная погрешность (БОЛЬШЕ) 0,0121101 - среднее значение
residuals. Durbin-Уотсон (СОБСТВЕННЫЙ ВЕС) статистические испытания residuals к
определите, есть ли любая существенная корреляция, основанная на заказе(порядке)
в котором они происходят в вашем файле данных. Так как P-значение больше
чем 0.05, нет никакой индикации относительно последовательной автокорреляции в
residuals.
В определении, может ли модель быть упрощена, обратите внимание что
самое высокое P-значение на независимых переменных - 0,0684, принадлежа
X1. Так как P-значение - меньше чем 0.10, тот срок(термин) - статистически
существенный на 90%-ом доверительном уровне. В зависимости от веры(секретности)
уровень, над которым Вы желаете работать, Вы может или не мочь решить удалять
X1 от модели.
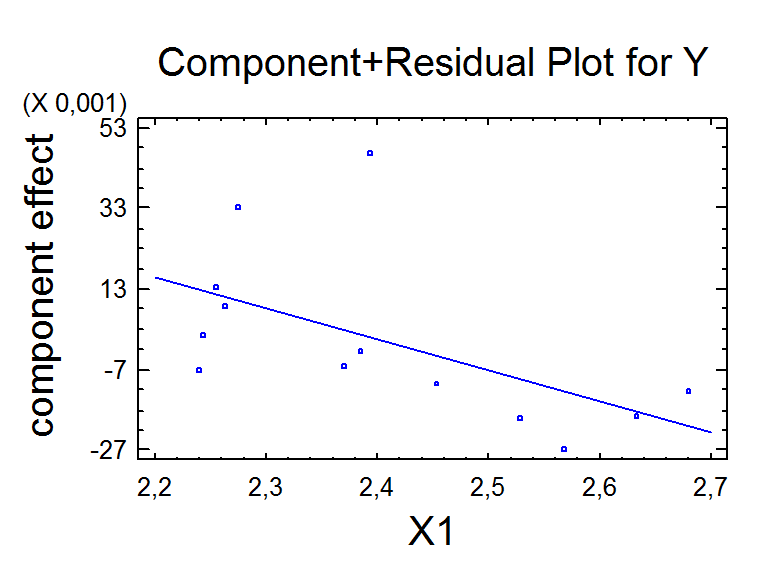
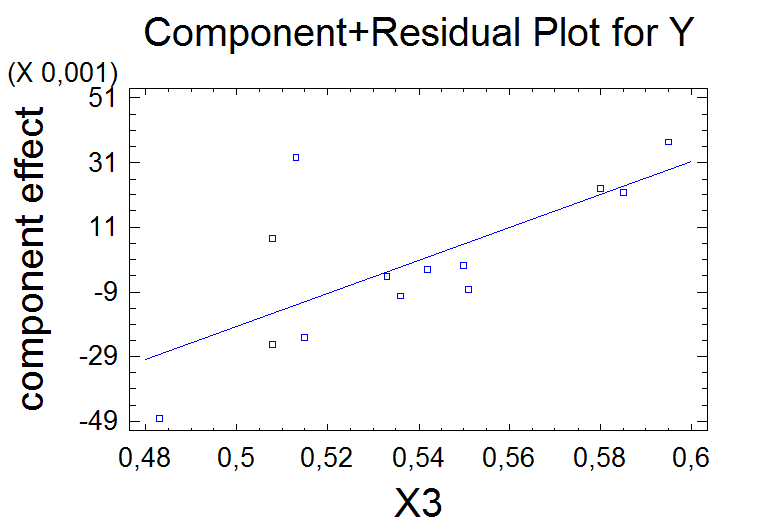
Этот график показывает части приспособленной модели, связывающей Y к X3.
Уравнение строки на графике
Y = 0,509772 * (X3-0,538385)
Строка показывает относительному изменению(замене) в предсказанных значениях Y который
происходит при изменении(замене) X3 по его наблюдаемому(соблюденному) диапазону. Каждый пункт(точка) – тогда составленный график, добавляя его остаточный к строке. Исследуя размер residuals относительно изменения(замены) в предсказанных значениях ответ, Вы можете судить важность выбранных независимого
переменная.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.