Модели управления запасами

Ожидаемые затраты на хранение вычисляются на основе ожидаемых наличных уровней запаса на начало и конец цикла. Ожидаемый уровень запаса в конце цикла равен E{R—х). В начале цикла (в момент поставки заказа размером у) ожидаемый уровень запаса равен y-\-E{R—х). Таким образом, средний уровень запаса за цикл (и, следовательно, за год) определяется выражением

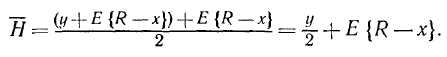
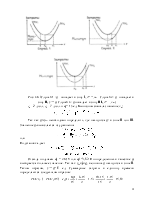
При указанной выше функции f{x)

Е {R — x} = \™(R —х) f (x) dx = R—E {x}.

Отметим, что в выражении для Н не учитывается случай, когда величина R—Е {х} отрицательная (размер дефицита), что является одним из  упрощающих допущений модели.

Пусть S— размер дефицита за  цикл.  Тогда

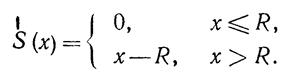
Следовательно, ожидаемый размер дефицита за цикл равен

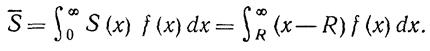
Так как в течение года размещается примерно (D/y) заказов, то ожидаемый годовой дефицит составляет (DSfy).

Таким образом, суммарные годовые затраты в системе описываются выражением

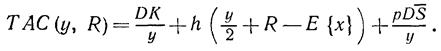
Отметим, что потери от дефицита (pDSly) предполагаются пропорциональными размеру дефицита только тогда, когда не учитывается продолжительность дефицита. Это также является упрощающим предположением в модели, так как в случае задолженности потери от дефицита зависят от его продолжительности.

Оптимальные значения у* и R* находятся из уравнений

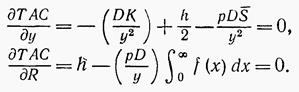
          Из первого уравнения имеем

                                                                                            (1)

а из второго

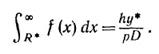                                                                                              (2)

В этом случае не удается получить общее решение для у* и /?* в явном виде. Поэтому для решения уравнений (1) и (2) используется числовой метод. Хедли и Уайтин доказали, что при существовании решения предложенный ими алгоритм сходится за конечное число итераций.

В уравнении (1) значение 5 не может быть меньше нуля, откуда следует, что минимальное значение у* равно \f2DKlhи достигается при 5=0 (или R-^oo). Но при R=0 уравнение (1) дает

а из уравнения (2) имеем

Можно доказать, что если у ≥ у, то оптимальные значения у и Rсуществуют и единственны. При этом условии значения у   и Rнаходятся следующим образом. Вычисляется первое пробное значение у*, равное . Далее, используя уравнение (2), вычисляют значение R_ltсоответствующее у_г. Используя найденное значение R₁ по уравнению (1) определяют новое пробное значение у_г. Затем по уравнению (2), в которое подставляется у₂, вновь вычисляется R₂. Процедура повторяется до тех пор, пока два последовательных значения Rне станут приблизительно равными. Найденные на последней итерации значения у и Rдают у* и R*.

7.2. Одноэтапные модели

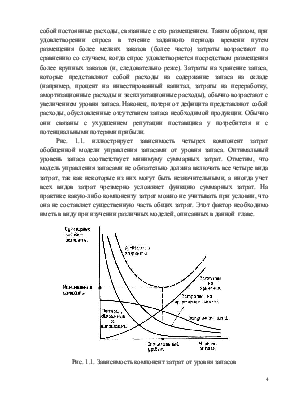
Одноэтапные модели управления запасами отражают ситуацию, когда для удовлетворения спроса в течение определенного интервала времени продукция заказывается только один раз. Например, модный товар устаревает, и, следовательно, заказы на него могут не возобновляться. В данном подразделе одноэтапные модели исследуются при различных предположениях, в том числе при мгновенном и равномерном спросе с учетом и без учета затрат на оформление заказов. Предполагается, что пополнение запаса осуществляется мгновенно. Оптимальный уровень запаса определяется, исходя из минимизации ожидаемых затрат на управление запасами, которые включают затраты на размещение заказа (затраты на оформление + затраты на закупку или производство), хранение и потери от дефицита. В связи с вероятностным характером спроса затраты на закупку (производство) единицы продукции, будучи постоянными, тем не менее становятся существенным фактором в функции общих затрат.

7.2.1. Мгновенный спрос при отсутствии затрат на оформление заказа

В моделях с мгновенным спросом предполагается, что суммарный спрос удовлетворяется в начале этапа. Таким образом, в зависимости от затребованного количества £ после момента возникновения спроса запас сразу может оказаться либо положительным (излишки), либо отрицательным (дефицит). Оба этих случая иллюстрирует рис. 3.10.

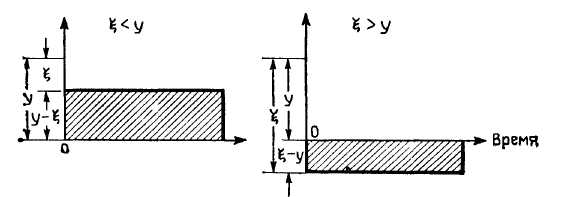
Из рис. 13.14следует, что при заданном у уровень запаса после поставки