Рассмотрим движение точки С относительно точки B, а затем по отношению к точке C’.
Ускорение точки С определяется графическим решением следующих двух векторных уравнений
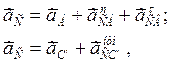 (2.13)
(2.13)
где ![]() ,
, ![]() – соответственно нормальная и
тангенциальная составляющие ускорения в движении точки С относительно
точки В;
– соответственно нормальная и
тангенциальная составляющие ускорения в движении точки С относительно
точки В;
![]() –
соответственно относительная составляющие ускорения в движении точки С
относительно точки C’.
–
соответственно относительная составляющие ускорения в движении точки С
относительно точки C’.
В первом уравнении нормальное ускорение ![]() направлено по звену ВC
(от точки С к точке В). Величина ускорения
направлено по звену ВC
(от точки С к точке В). Величина ускорения
![]() (2.14)
(2.14)
или,
учитывая, что 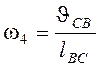 , получим
, получим
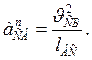 (2.14а)
(2.14а)
Подставляя численные значения в (2.14), получим
![]()
На плане ускорений через точку b
проводим прямую, параллельную звену ВC и
откладываем на ней в направлении от точки C к точке B
вектор ![]() , представляющий в масштабе
, представляющий в масштабе ![]() ускорение
ускорение ![]()
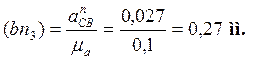
Через точку n3 проводим прямую в направлении тангенциального ускорения
![]() перпендикулярно к звену ВC.
перпендикулярно к звену ВC.
Во втором уравнении нормальное ускорение ![]() направлено по звену CC’ (от точки С к точке C’).
направлено по звену CC’ (от точки С к точке C’).
На плане ускорений через полюс p и совпадающую с ним точку c’ (ускорение опоры C’ ![]() ) проводим прямую,
параллельную CC’ и откладываем
на ней в направлении от точки C к точке C’ вектор, представляющий в масштабе
) проводим прямую,
параллельную CC’ и откладываем
на ней в направлении от точки C к точке C’ вектор, представляющий в масштабе ![]() ускорение
ускорение ![]()
Точка с пересечения двух тангенциальных прямых определяет конец вектора полного ускорения точки С, соединив ее с полюсом p, определим величину данного ускорения
![]()
Величины тангенциальных ускорений соответственно равны
![]()
По правилу сложения векторов ![]() и
и
![]() соединяем на плане ускорений точки b
и c и получим вектор полного ускорения звена ВC.
соединяем на плане ускорений точки b
и c и получим вектор полного ускорения звена ВC.
![]() (2.16)
(2.16)
Его величина определяется как
![]() (2.17)
(2.17)
Подставляя численные значения, получим
![]()
Ускорение центра масс S4 звена 4 определяется с помощью теоремы подобия
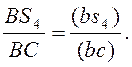
Откуда
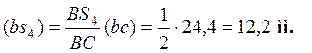
На плане ускорений отложим на векторе ![]() от точки b отрезок (bs4), длиной 12,2 мм. Соединив точку s4 с
полюсом p, получим вектор ускорения центра масс S4 звена 4. Тогда
от точки b отрезок (bs4), длиной 12,2 мм. Соединив точку s4 с
полюсом p, получим вектор ускорения центра масс S4 звена 4. Тогда
![]()
Все векторы, выходящие из полюса p на плане ускорений, изображают абсолютные ускорения, а отрезки, соединяющие концы векторов – относительные ускорения точек.
Определим величины угловых ускорений звеньев, используя следующую зависимость
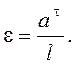 (2.18)
(2.18)
Подставляя численные значения, для рассматриваемого положения механизма получим
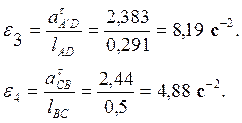
Направление углового ускорения ![]() шатуна
2 определим, если перенесем вектор
шатуна
2 определим, если перенесем вектор ![]() из плана ускорений в
точку В звена АВ. Под действием этого вектора звено АВ
будет вращаться вокруг точки А против часовой стрелки.
из плана ускорений в
точку В звена АВ. Под действием этого вектора звено АВ
будет вращаться вокруг точки А против часовой стрелки.
Направление углового ускорения ![]() звена
4 определит вектор
звена
4 определит вектор ![]() , перенесенный из плана ускорений
в точку С звена ВС, а углового ускорения
, перенесенный из плана ускорений
в точку С звена ВС, а углового ускорения ![]() –
вектор
–
вектор ![]() , также перенесенный в точку С,
принадлежащей звену DC.
, также перенесенный в точку С,
принадлежащей звену DC.
2.4 Построение кинематических диаграмм для точки С
2.4.1 Диаграмма перемещения
На оси абсцисс откладываем отрезок l, изображающий время одного оборота кривошипа, и делим его на 12 равных частей, а в соответствующих точках откладываем перемещения точки В от начала отсчета из плана положений механизма.
Масштаб по оси ординат определяется как
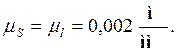
Масштаб по оси абсцисс определим по формуле
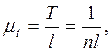 (2.19)
(2.19)
где Т – период оборота начального звена;
n – частота вращения начального звена.
Подставляя численные значения, получим
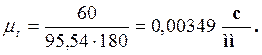
2.4.2 Диаграмма скоростей
Диаграмма скоростей точки В строится по данным
планов скоростей путем переноса длин векторов скоростей точки В на
соответствующие ординаты диаграммы скоростей. Масштаб по оси ординат ![]() принят равным масштабу
принят равным масштабу ![]() планов скоростей
планов скоростей
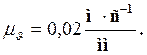
2.4.3 Диаграмма ускорений
Диаграмма ускорений построена графическим дифференцированием (методом хорд) диаграммы скоростей. Полюсное расстояние ОР принимается из соображения загруженности чертежа. При этом следует учесть, что чем больше полюсное расстояние, тем большее место диаграмма будет занимать на чертеже. Поэтому полюсное расстояние принимается таким, чтобы диаграмма не выходила за пределы листа и не пересекала диаграмму скоростей. Для нашего случая полюсное расстояние принято равным
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.