1. Показатели динамики.
2. Показатели структуры.
3. Показатели координации.
4. Показатели интенсивности развития.
5. Показатели выполнения плана.
Показатели динамики используются для характеристики изменения явления во времени. Вычисляются путем отношения величины текущего периода к величине одного из предыдущих (базисных) периодов. Пример по Польше.
2. Характеризуют удельный вес отдельных составных элементов совокупности в общем итоге выраженной в процентах.
Показатели координации получают в рез сравнения отдельных частей целого между собой.
Относительные показатели интенсивности развития получают путем сравнения объемов разных совокупностей, находящихся в определенной связи друг с другом.
Относительная величина выполнения плана. Показ на сколько реальные показатели соответствуют плановому заданию. Если по плану фирмы оборот должен составить 5 млн. руб, а по факту –5,2 млн. руб à пок = 5,2/5=1,04=104%.
Средняя величина – обобщающий показатель характеризующий типичный уровень варьирующего признака для единиц данной совокупности. В средних величинах погашаются индивидуальные различия единиц совокупности обусловленные случайными обстоятельствами и находят выражение общие закономерные черты свойственные всей совокупности явления.
Основным условием правильного подсчета средней величины является качественная однородность совокупности. Перед расчетом средних, единицы совокупности должны быть разбиты на однородные группы, по которым рассчитывается средняя величина.
12. Средние величины: их сущность и знач, осн требования к подсчету средних.
Средне арифметическое, геометрическое, гармоническое, мода, медиана.
Средне арифметическая – исходная форма средних величин.
СА простая – x=åx/n. Пусть заключены договоренности на поставку 100 тонн азотистых удобрений. 1 – 135$ за тонну, 140, 150$ соответственно. Цена – варьирующий признак. 134+140+150/3 = 141,7$. Среднеарифметическую простую используют только тогда, когда значение вариантов встречаются по одному или по одинаковому числу раз. Если отдельные варианты признака повторяются не одинаковое число раз, т.е. имеют разный вес в совокупности, то используется формула среднеарифметической взвешенной. X=åxf/åf.
До 700$ - 10стр 0 350
700-2000 –7 = 1350
2000-5000 – 6 = 3500
5000-10000-127500
больше 10000 15 стр. 12500
Сначала найти середины всех промежутков. = 6229
Средняя геометрическая используется для определения средних коэффициентов и средних темпов роста показателей за определенный период времени. Рассчитывается по коэффициентам роста. X= корень n-ой степени из x1+x2+xn.
У1 – абсолютная величина показателя за последний год изучаемого периода, а у0 – первый год периода, тогда x1 = корень степени n-1 из у1/у0.
Средняя гармоническая
![]()
1. 5руб./шт. 500руб.
2. 10руб/шт. 2000 руб.
3. 15руб/шт. 4500.
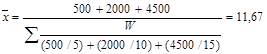
Мода – значение признака, которое чаще всего встречается в статистическом ряду.
В течении года было заключено 45 контрактов. 3 контракта по 243$ за тонну. 24-245, 4-246, 12-250, 2 – 254. В данном случае число 245- мода.
Медиана – знач признака, кот находится в середине непрерывно возрастающего или убывающего вариационного ряда. Медиана делит ряд пополам и по обе стороны от нее находится одинаковое кол-во единиц совокупн-ти.
243;243;243;245;245…..254
Медиана будет 23им показателем. Она раздел ряд пополам и по обе стороны будет равное кол-во показателей. Общая формула: Mo=(x1+x2+…+xn)/2+1/2. Роль x выполняют частоты.
Медиана и мода нужны в маркетинговых исследованиях.
13. Стат ряды, их виды и осн приемы анализа.
Статистические ряды – упорядоченные числа по определенному признаку.
Корреляционные ряды по убыванию признака.
Динамические ряды – изменение величины по годам (как величина изменялась во времени.
Вариационные – упорядоченное распределение единиц совокупности по возрастанию или убыванию варьирующего.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.