Синтез преобразователей кодов

1.5 Синтез преобразователей кодов

 Синтез преобразователей кодов производится двумя методами.

 Первый метод основан на преобразовании исходного двоичного кода в десятичный и последующего преобразования десятичного кода в требуемый двоичный. Этот метод реализуется путём соединения дешифратора и шифратора, составленным по рассмотренным здесь способам. Удобство этого метода очевидно, когда имеются стандартные дешифраторы и шифраторы в интегральном исполнении.

 Второй метод заключается в синтезе комбинационного устройства, непосредственно осуществляющего преобразование одного двоичного кода в другой.

 Рассмотрим этот метод на примере преобразования кода 8421 в код 3а+2.

 Рассматриваемые коды приведены в табл. 2.0. Каждая переменная Y нового кода может рассматриваться как функция от переменных X₄ ,X₃ ,X₂ ,X₁  преобразуемого кода.

Таблица 2.0.

Истинность для кодов

 Эти функции запишутся в виде формул:

Y₅ =++++;

Y₄ =++++;

Y₃ =++++;

Y₂ =++++;

Y₁ =++++;

 Поскольку полученные функции представлены в СДНФ, то для их минимизации используются карты Карно ( Вейча ) рис. 2.1.

 После проведения операций склеивания по известным правилам получим МДНФ:

Y₅=;

Y₄=;

Y₃=;

Y₂=;

Y₁=.

 Эти функции можно реализовать на элементах базиса И, ИЛИ, НЕ.

 В то же время, минимизировав функции по методу Карно, мы можем  не получить минимизированной схемы преобразователя, поскольку каждая из функций Y₁ , ... , Y₅ должна быть реализована отдельно.

 Рациональнее в этом случае для получения минимизированной схемы использовать метод Квайна, порядок которого изложен ранее.

 Для минимизации составим таблицы, аналогичные табл. 1.3-1.7, и в результате определим минимизированные функции, описывающие структуру преобразователя кодов:

Y₅=;

Y₄=;

Y₃=;

Y₂=;

Y₁=.

 Несмотря на то, что общее количество букв больше, чем в формулах, полученных методом Карно, устройство будет содержать меньшее количество элементов, поскольку некоторые члены полученных выражений повторяются в различных функциях, то есть имеется возможность неоднократного использования одних и тех же элементов преобразователя кодов.

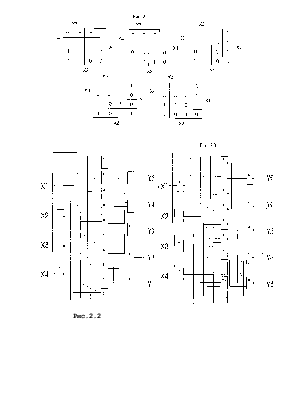
 Схема преобразователя на элементах базиса И, ИЛИ, НЕ представлена на рис. 2.2.

 Для того, чтобы реализовать схему преобразователя кодов на элементах базисов И, НЕ или ИЛИ, НЕ, необходимо представить полученные выражения для Y₁ , ... , Y₅ в форме функций Шеффера или Вебба соответственно ( см. п. 1.2 )

 Так, в выражениях Шеффера:

Y₅=;

Y₄=;

Y₃=;

Y₂=;

Y₁=.

а в выражениях Вебба:

Y₅=;

Y₄=;

Y₃=;

Y₂=;

Y₁=.

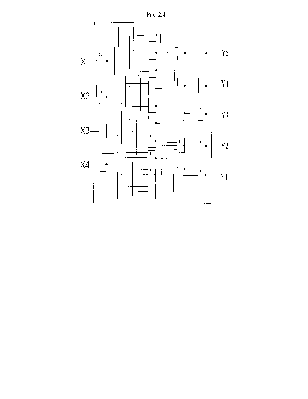
Схемы преобразователей кодов на элементах И-НЕ и ИЛИ-НЕ показаны на рис. 2.3 и 2.4.

 Аналогичным образом можно составить схемы преобразователей любого двоичного кода.                                             

    Рис.2.2