Решение уравнения 2ех+3х-1=0 приближёнными методами. Построение графика функции с помощью табличного процессора Еxсel

Министерство образования Республики Беларусь

Белорусский Государственный Университет Транспорта

Кафедра “Информационные технологии ”

Расчетно-графическая работа

по дисциплине «Информатика и информационные технологии»

Принял:                      Выполнила:

Захаров Д.В.                 студент гр. ЭМ-11

                          Сиволап Е.С.

                         2005

Задание

                     На расчетно-графическую работу по дисциплине                        

“Информатика”.

 Задание № 1

Номер варианта	Уравнение	Метод уточнения корней на          ПЭВМ
16	2ех+3х-1=0	Метод половинного деления

 Задание № 2

                          Шифр(7.1)

 Ввести массив z[0..3] и a[0..3]. Для каждого z[0..3] и a[0..3] вычислить . Найти сумму значений элементов массивов z и a. Исходный массив и результаты распечатать.

Задание выдано 25.02.2002.

Срок выполнения 1.06.2002.

Руководитель работы Гагина Л.Н.               

Содержание

1  Решение уравнение приближёнными методами.

1.1 Отделение корней уравнения на интервале C1,D1  с шагом h.

1.2 Построение графиков функции на интервале C1,D1.

1.3 Уточнение корней уравнения с помощью пакета Mathcad.

1.4  Уточнение корней уравнения методом половинного деления.

1.4.1 Описание используемого метода уточнения корней.

1.4.2 Блок-схема алгоритма.

1.4.3 Трассировка алгоритма с помощью пакета Mathcad.

1.4.4 Программа на языке Pascal и результаты решения.

2  Решение нестандартной задачи на языке Pascal.

2.1 Блок-схема алгоритма.

2.2 Трассировка алгоритма.

2.3 Программа на языке Pascal и результаты расчёта.

3  Построение графиков функции с помощью табличного                                                                                

процессораEXCEL.

1.  Решение уравнения приближенными методами.

1.1 Отделение корней уравнения на интервале C1,D1 с шагом h.

Program otd_kor_a1_b1;

Var a1,b1,x,y1,y2,h:real;

    Function F(t:real):real;

Begin

           F:=2*exp(x)+3*x-1;

        end;

   Begin

        Write('введите начало ,конец отрезка и шаг');

         Readln(a1,b1,h);

              y1:=F(a1);

              x:=a1;

         Repeat

              x:=x+h;

              y2:=F(x);

                  If y1*y2<0 then

Writeln('a=',x-h:4:2,'   F(a)=',y1:9:6,'      b=',x:4:2,'   F(b)=',y2:9:6);

              y1:=y2;

          until x>b1;

    end.

введите начало ,конец отрезка и шаг

-4

2

0.2

a=-0.4   F(a)=-0.859000     b=-0.2    F(b)= 0.037000

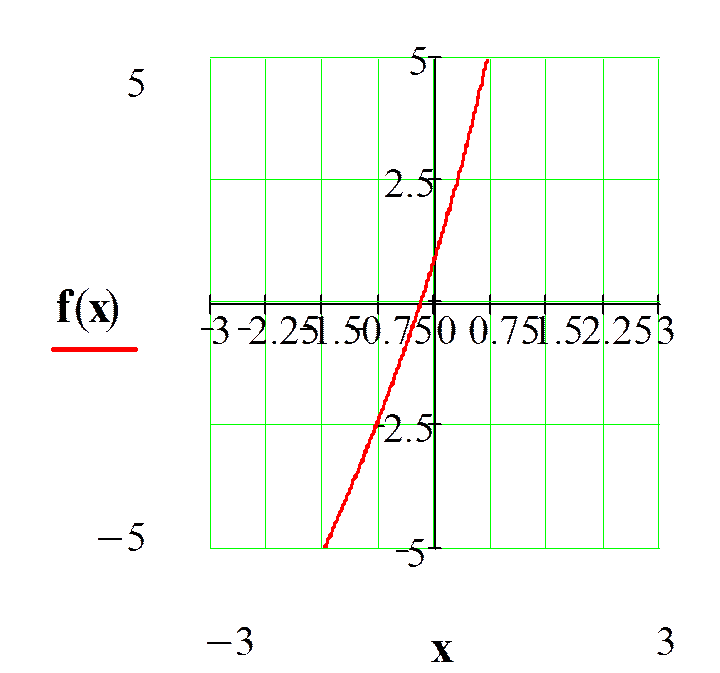
1.2 Построение графика функции

       2е^х+3х-1=0

на интервале С1,D1.на интервале С1,D1.

1.3 Уточнение корней уравнения с помощью пакета Mathcad.

1.4  Уточнение корней уравнения методом половинного деления;

1.4.1  Описание используемого метода уточнения корней;

Решение уравнения распадается на два этапа:

1)  отделение корней уравнения;

2)  уточнение корней уравнения.

При решении задачи с помощью языка программирования Pascal используется метод половинного деления.

Геометрический смысл метода половинного деления. При отделении действительного корня уравнения получили, что Х^* є [a, b]. Для уточнения корня методом половинного деления делим отрезок [a, b] пополам и вычисляем значения функции в середине отрезка f(X_cp), где X_cp=(a+b)/2. Если f(X_cp)=0 (Рисунок 1.), то, следовательно, Xcp=X^* и процесс заканчивается; если f(X_cp)=0, то знак f(X_cp) совпадает либо со знаком f(a), либо со знаком f(b), так как корень находится на отрезке [a, b] и функция f(X) на концах этого отрезка должна иметь разные знаки.

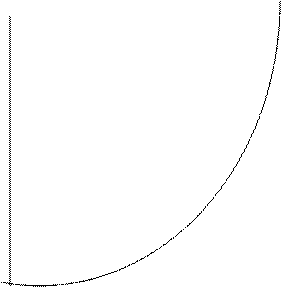
Пусть X_cp=X₁ и знак функции f (X₁) совпадает со знаком функции f(b) (Рисунок 2), тогда отрезок [X₁, b] можно не рассматривать дальше, на нем корня не будет, так как

 

     Y                                                               B                               

 

                                                           f(b)

                   A              Xcp                                                                        

                                                          B