Решение распределительных задач оптимизации (Лабораторная работа № 3), страница 5

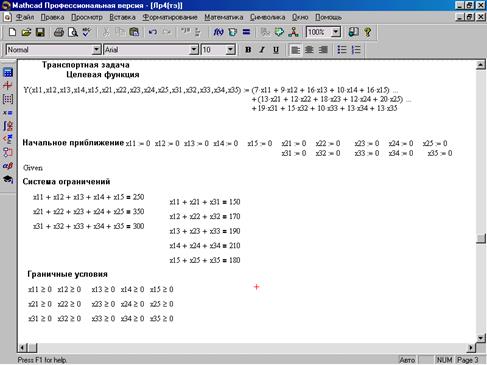
Рисунок 1. Решение транспортной задачи в MathCad2000

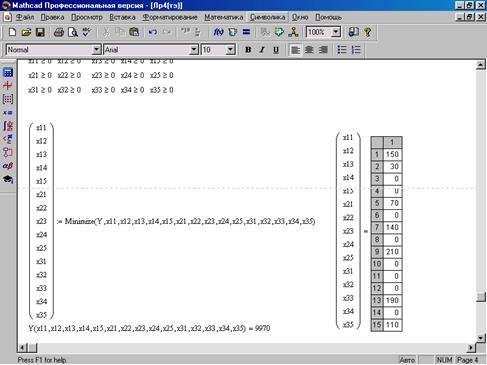
Рисунок 2. Решение транспортной задачи в MathCad2000

Получен вектор оптимальных значений, который означает, что из первого 1-го отправления ресурс нужно поставлять в 1-й, 2-й и 5-й пункты назначения в объемах 150, 30 и 70 единиц ресурса соответственно; из 2-го пункта отправления ресурс нужно поставлять во 2-й, и 4-й пункты назначения в объемах 140, 210, а из 3-го пункта отправления - во 3-й и 5-й пункты назначения в объемах 190, и 110 соответственно. При этом суммарные затраты на перевозку всех ресурсов будут минимальны и составят 9970 единиц.

Таблица 2

Решение транспортной задачи в Excel

Порядок решения задачи следующий:

1. Ввести название работы;
2. В ячейки с адресами B3:F5 введите значения стоимости работ в виде исходной матрицы задачи;
3. Выделить область изменяемых ячеек – это диапазон B7:F9 и закрасить для наглядности любым цветом;
4. В ячейку с адресом E13 введите целевую функцию. Для этого нажмите на знак “=” и в строке состояния слева из списка математических функций выберите функцию СУММПРОИЗ(), аргументами которой выберите сначала матрицу стоимости работ (диапазон B3:F5), а затем область изменяемых переменных (диапазон B7:F9) и нажмите кнопку “Ok”. В результате в ячейке E10 появится: СУММПРОИЗ (B7:F9, B3:F5) (рис.3);
5. Справа и внизу от области выделяемых значений вводим ограничения задачи: для этого нажимаем знак “=” и выбираем из списка математических функций функцию суммирования: СУММ(), аргументами которой является сначала первая строка области изменяемых ячеек (B7:F7), т.е. СУММ (B7:F7). Аналогично вводим остальные ограничения по всем строкам и столбцам (рис.3);
6. Справа и внизу от ограничений вводим значения правой части ограничений;
7. Выполняем команду Сервис – Поиск решения. Если в меню Сервис такой команды нет, то выполняем надстройку. Для этого выбираем команду Сервис – Надстройки и включаем флажок напротив надписи “Поиск решения”;
8. Заполнить окно Сервис – Поиск решения (рис. 3):

·  Установить целевую ячейку – E13;

·  Задать равенство минимальному значению;

·  Задать адреса изменяемых ячеек: B7:F9;

·  Добавить ограничения. Нажать кнопку “Добавить”. В появившемся окне слева задать адреса диапазона, где введены формулы для ограничений (диапазон G7:G9), далее выбрать знак “=” и выделить диапазон правых частей для ограничений, т.е. столбец единиц (H7:H9). Аналогично выделить диапазон A10:F10, выбрать знак “=” и выделить A11:F11. Нажать кнопку “Добавить”.

·  Заполнить окно параметров поиска решений. Нажать кнопку “Параметры” и установить флажком линейную модель оптимизационной задачи и неотрицательные значения для значения переменных.

·  Нажать кнопку “Выполнить” и закрашенных ячейках, при правильном вводе исходных значений и задании ограничений и других параметров появится оптимальное решение.

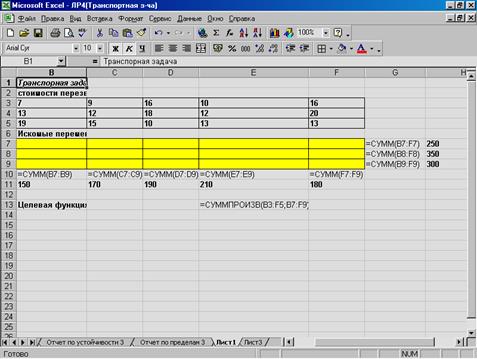
Рисунок 3. Решение транспортной задачи в MS Excel

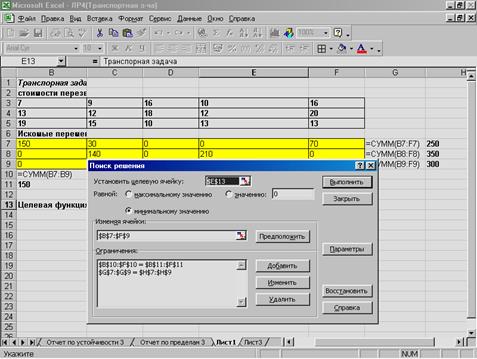
Рисунок 4. Заполнение окна “Поиск решения”