Решение распределительных задач оптимизации (Лабораторная работа № 3), страница 4

·  Установить целевую ячейку – E10;

·  Задать равенство максимальному значению;

·  Задать адреса изменяемых ячеек: B7:D9;

·  Добавить ограничения. Нажать кнопку “Добавить”. В появившемся окне слева задать адреса диапазона, где введены формулы для ограничений (диапазон B12:B17), далее выбрать знак “=” и выделить диапазон правых частей для ограничений, т.е. столбец единиц (С12:С17). Нажать кнопку “Ok”.

·  Заполнить окно параметров поиска решений. Нажать кнопку “Параметры” и установить флажком линейную модель оптимизационной задачи и неотрицательные значения для значения переменных.

Рассмотрим подробнее окно параметров поиска решений.

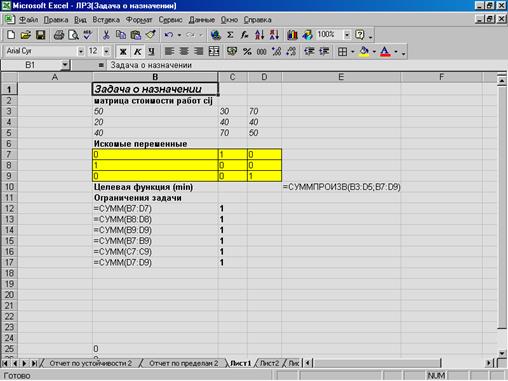
Рисунок 2. Решение задачи о назначении в MS Excel

ТРАНСПОРТНАЯ ЗАДАЧА

Постановка задачи. Пусть имеется m=3 пунктов отправления A_i и n=5 пунктов назначения B_j некоторого ресурса. Пусть также известно количество ресурсов в i-ом пункте отправления (a_i) и потребность в этом ресурсе в j-ом пункте назначения (b_j). Известны также затраты на перевозку одной единицы ресурса из каждого i-го пункта отправления в каждый j-ый пункт назначения. Требуется определить, какое количество ресурсов  x_ij (x_ij ³0) необходимо поставить из каждого i-го пункта отправления в каждый пункт j–ый назначения, чтобы вывести все ресурсы из всех пунктов отправления, обеспечить все пункты назначения данным видом ресурсов и перевозки выполнить с минимальными затратами.

Математическая модель задачи

Пусть общий объем поставляемых ресурсов равен общему объему потребляемых ресурсов, т.е.

В такой постановке задача называется сбалансированной и в этом случае ее можно решить методом потенциалов.

Ограничения задачи:

1. Ресурсы всех источников (пунктов отправления) должны быть реализованы:

2. Запросы всех пунктов потребления должны быть удовлетворены:

3. Целевая функция: транспортные расходы должны быть минимальны

Задача (2)-(4) является специальной задачей линейного программирования и называется транспортной задачей.

Для исходной задачи математическая модель имеет следующий вид:

Способы решения задачи

Решение транспортной задачи средствами MathCad 2000

Порядок решения задачи следующий:

1. Введем сначала поясняющий текст в рабочем листе. Для этого расположим  курсор (визир - красный крестик) в месте ввода текста. Затем выберем (щелчком мыши или с помощью клавиатуры) пункт Insert (Вставка) главного меню МаthCаd. В появившемся падающем меню выберем пункт Техt Rеgion (Текстовая область) или в месте расположения курсора нажмем клавишу с двойной кавычкой (команда для ввода текста). В обоих случаях появится шаблон, указывающий, место и начало ввода текста, который и будет введен после этого. Текстовая область начнет автоматически увеличиваться по мере ввода текста. По окончании этой операции выведем курсор (маркер ввода - красная вертикальная черточка) за рамки текстовой области.
2. Далее введем критерий оптимизации - целевую функцию. Для этого вначале разместим курсор в месте ввода математического выражения. Сначала введем имя критерия оптимизации с аргументами, записанными через запятые и заключенными в скобки. Далее нажмем комбинацию клавиш: Shift+”:” (двоеточие) для ввода знака присваивания ”:=”.
3. Аналогично вводятся начальные приближения.
4. Для решения задачи используем блок функцийGiven...Minimize. Для этого нужно ввестиGiven.
5. Далее следует ввести систему ограничений. При вводе её используйте жирный знак равенства, вызвать его можно нажатием комбинации клавишCtrl + ”=”и ввести граничные значения (рис. 1).
6. Введите вектор-столбец искомых параметров, используя диалоговое окно Insert Matrix (Вставить Матрицу). Для этого щелкните по кнопке на панели инструментов Маtrix (Матрица) или нажмите комбинацию клавиш Сtrl+”М”. В появившемся диалоговом окне введите размерность для вектора столбца: в поле строки (Rows) введите 15, а в поле столбцы (Со1umns) - 1; и ввести знак присваивания; Далее введите функцию Мinimize с искомыми параметрами, используя диалоговое окноInsert - Function (Вставить функцию), вызвав его нажатием комбинации клавиш Сtrl+”F”;