Информатика и выч. техника \ Математические модели в расчетах на ЭВМ

Решение распределительных задач оптимизации (Лабораторная работа № 3), страница 3

В качестве критерия оптимизации принята суммарная себестоимость выполнения всех работ. Обозначим через cij себестоимость возведения i-го объекта j-м краном. Тогда критерий оптимизации Z - суммарная себестоимость выполнение всех работ запишется в таком виде:

.

(3)

Совокупность ограничений (1) и (2) и целевой функции (3) образует математическую модель типичной экстремальной комбинаторной задачи. Ее решение представляет собой некоторую перестановку чисел, а количество перестановок с ростом n резко возрастает и равно n!. Для нашей задачи n = 5! == 120, а для n = 7 число перестановок составляет 5040. В научно-технической литературе эта задача имеет название - задача о назначении.

Она относится к классу задач линейного программирования, так как ограничения и целевая функция имеют линейный вид, то есть искомые величины находятся в первой степени.

Способы решения задачи

Решение задачи с использованием системы МаthCаd 2000

Замечание: Для решения задачи о назначении ограничимся матрицей 3 на 3.

Порядок решения задачи следующий:

1.  Введем сначала поясняющий текст в рабочем листе. Для этого расположим  курсор (визир - красный крестик) в месте ввода текста. Затем выберем (щелчком мыши или с помощью клавиатуры) пункт Insert (Вставка) главного меню МаthCаd. В появившемся падающем меню выберем пункт Техt Rеgion (Текстовая область) или в месте расположения курсора нажмем клавишу с двойной кавычкой (команда для ввода текста). В обоих случаях появится шаблон, указывающий, место и начало ввода текста, который и будет введен после этого. Текстовая область начнет автоматически увеличиваться по мере ввода текста. По окончании этой операции выведем курсор (маркер ввода - красная вертикальная черточка) за рамки текстовой области.

2.  Далее введем критерий оптимизации - целевую функцию. Для этого вначале разместим курсор в месте ввода математического выражения. Сначала введем имя критерия оптимизации с аргументами, записанными через запятые и заключенными в скобки. Далее нажмем комбинацию клавиш: Shift+”:” (двоеточие) для ввода знака присваивания ”:=”.

3.  Аналогично вводятся начальные приближения.

4.  Для решения задачи используем блок функцийGiven...Minimize. Для этого нужно ввестиGiven.

5.  Далее следует ввести систему ограничений. При вводе её используйте жирный знак равенства, вызвать его можно нажатием комбинации клавишCtrl + ”=”и ввести граничные значения (рис. 1).

6.  Введите вектор-столбец искомых параметров, используя диалоговое окно Insert Matrix (Вставить Матрицу). Для этого щелкните по кнопке на панели инструментов Маtrix (Матрица) или нажмите комбинацию клавиш Сtrl+”М”. В появившемся диалоговом окне введите размерность для вектора столбца: в поле строки (Rows) введите 9, а в поле столбцы (Со1umns) - 1; и ввести знак присваивания; Далее введите функцию Мinimize с искомыми параметрами, используя диалоговое окноInsert - Function (Вставить функцию), вызвав его нажатием комбинации клавиш С1г1+”F”;

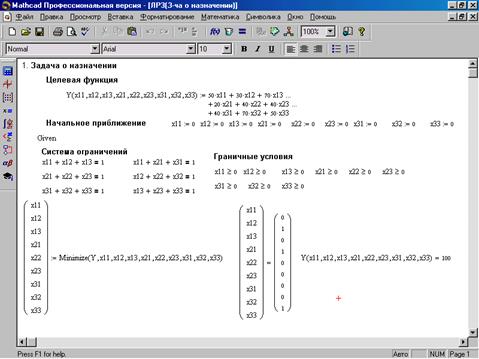
Рисунок 1. Решение задачи о назначении в MathCad

На рисунке 1. показан процесс и результат решения задачи о назначении встроенными средствами оптимизации пакета MathCad. Получен вектор оптимальных значений, который означает, что первый кран должен возводить второй объект, второй – первый, а третий кран – третий объект. При этом суммарные затраты на возведение всех объектов будут минимальны и составят 100 единиц.

Решение задачи с использованием MS Excel

Порядок решения задачи следующий:

  1. Ввести название работы;
  2. В ячейки с адресами B3:D5 введите значения стоимости работ в виде исходной матрицы задачи;
  3. Выделить область изменяемых ячеек – это диапазон B7:D9 и закрасить для наглядности любым цветом;
  4. В ячейку с адресом E10 введите целевую функцию. Для этого нажмите на знак “=” и в строке состояния слева из списка математических функций выберите функцию СУММПРОИЗ(), аргументами которой выберите сначала матрицу стоимости работ (диапазон B3:D5), а затем область изменяемых переменных (диапазон B7:D9) и нажмите кнопку “Ok”. В результате в ячейке E10 появится: СУММПРОИЗ(B7:D9, B3:D5) (рис.1);
  5. Введите комментарии для ограничений;
  6. Далее вводим ограничения задачи: для этого нажимаем знак “=” и выбираем из списка математических функций функцию суммирования: СУММ(), аргументами которой является сначала первая строка области изменяемых ячеек (B7:D7), т.е. СУММ(B7:D7). Аналогично вводим остальные ограничения по всем строкам и столбцам (рис.2);
  7. Справа от столбца ограничений вводим значения правой части ограничений, т.е. столбец из единиц;
  8. Выполняем команду Сервис – Поиск решения. Если в меню Сервис такой команды нет, то выполняем надстройку. Для этого выбираем команду Сервис – Надстройки и включаем флажок напротив надписи “Поиск решения”;
  9. Заполнить окно Сервис – Поиск решения:
Скачать файл