Решение нелинейных уравнений приближенными методами и нестандартных задач

 

Номер варианта	Уравнение	Метод уточнения корней	Точность
13	1.5*Х-3*ln(X)-4	Метод половинного деления	0.001

Содержание

Введение

1.  Отделение корней уравнения на большом интервале [a1, b1] с шагом h=0,1

1.1.  Графическая иллюстрация

1.2.  *Блок-схема алгоритма

1.3.  Программа на языке Паскаль и результаты расчетов

2.  Уточнение корней уравнения методом половинного деления

2.1.  Графическая  иллюстрация метода половинного деления

2.2.  *Блок-схема алгоритма

2.3.  Программа на языке Паскаль и результаты расчетов

3.  Решение уравнения средствами пакета MATHCAD

3.1.  Построение графика функции

3.2.  Уточнение корней уравнения

4.  Решение уравнения с помощью табличного процессора Excel

5.  *Знакомство с сетью Internet. Формирование Web-документа, его пересылка на сайт кафедры и работа с этим документом с помощью сети Internet

6.  *Презентация РГР

7.  Вывод по работе

Литература

* - не обязательно

Введение

          Процедура подготовки и решения задачи на ЭВМ состоит из нескольких этапов.

Сначала необходимо разработать алгоритм решения задачи. Алгоритм – последовательность арифметических и логических действий над числовыми значениями переменных, приводящая к вычислению результата решения задачи при изменении исходных данных в достаточно широких пределах. Он обладает следующими свойствами: детерминированностью, означающей, что применение алгоритма к одним и тем же исходным данным должно приводить к одному и тому же результату; массовостью, позволяющей получать результат при различных исходных данных; результативностью, обеспечивающей получение результата через конечное число шагов.

Наиболее наглядным способом описания алгоритмов – является описание его в виде схем. При этом, алгоритм представляется последовательностью блоков, выполняющих определённые функции, и связей между ними. Внутри блоков указывается информация, характеризующая выполняемые ими функциями.

Затем составляется программа на одном из языков программирования. При описании программ необходимо использовать характерные приёмы программирования и учитывать специфику конкретного языка.

При отладке программы происходит обнаружение и исправлении ошибок, допущенных на всех этапах подготовки задач к решению на ЭВМ. Синтаксические ошибки обнаруживаются транслятором, который выдаёт сообщение, указывающее место и тип ошибки. Обнаружение семантических ошибок осуществляется на этапе тестирования программы, в котором проверяется правильность выполнения программы на упрощённом варианте исходных данных или с помощью контрольных точек.

Обработка результатов решения задачи осуществляется либо с помощью ЭВМ, либо вручную. Выводимые результаты оформляются в виде, удобном для восприятия человеком.

1. Отделение корней уравнения на большом интервале [a1, b1] с шагом h=0,1

1.1  Графическая иллюстрация

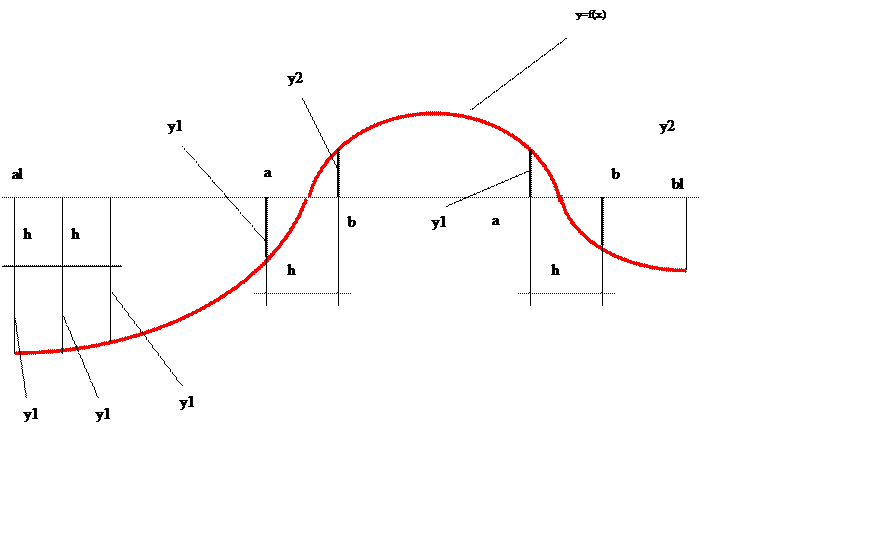                                 Пояснения

a1,b1- большой интервал, внутри которого исследуются корни уравнения f(x)=0

a, b-интервалы размером h, внутри которых находятся корни заданных уравнения

Найти интервалы [a, b]- этот процесс называется отделением корней уравнения

y1- значение функции в начале шага

y2- значение функции в конце шага

1.2. *Блок-схема алгоритма

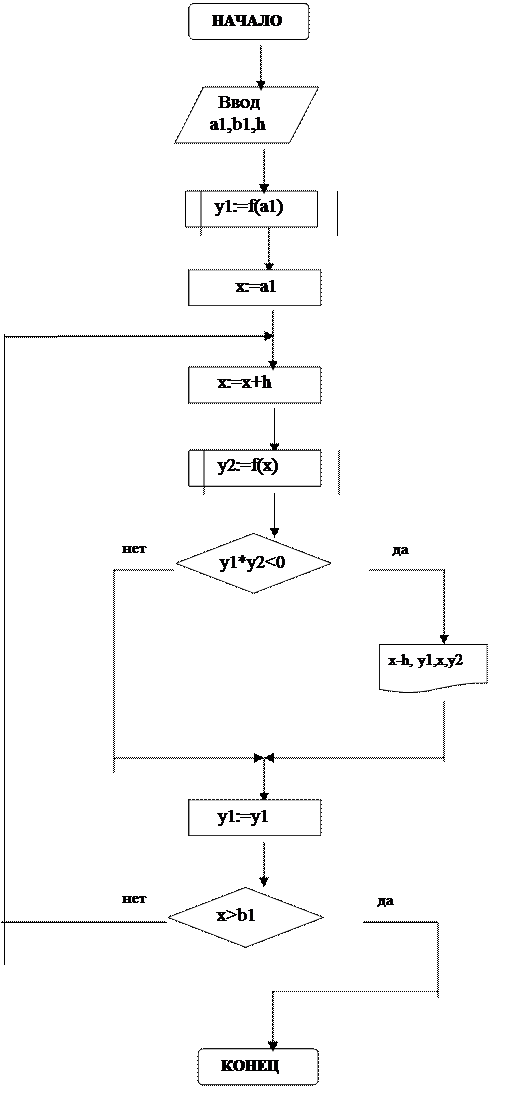1.3. Программа на языке Паскаль и результаты расчетов

 Program otdelenie_korney;

var a1,b1,h,x,y1,y2:real;fp:text;

 Function FUR (t:real):real;

  begin

   FUR:=1.5*Х-3*ln(X)-4;

  end;

Begin

 assign(fp,'a:\otdkor.pas');

 append(fp);

 write('Введите a1,b1,h: ');

   readln (a1,b1,h);

      y1:=FUR(a1);

      x:=a1;

   repeat

      x:=x+h;

      y2:=FUR(x);

      if y2*y1<0 then writeln (fp, 'a1= ',x-h:4:1,'   F(a1)= ',y1:9:6,

      '     b1= ',x:4:1,'   F(b1)=',y2:9:6);

      y1:=y2;

    until x>b1;

    close (fp);

    readln

    end.

2. Уточнение корней уравнения методом половинного деления

2.1. Графическая  иллюстрация метода половинного деления

   Геометрическим смыслом половинного деления является следующее:

при отделении действительного корня уравнения получили, что х принадлежит отрезку [a;b]. Для уточнения корня методом половинного деления делим отрезок [a;b] и вычисляем значение функции в середине отрезка