Расчёт линейной электрической цепи постоянного тока

   «Расчёт линейной электрической цепи постоянного тока»

                                         Шифр: 125

1) Для заданной электрической цепи рассчитать токи во всех ветвях:

а) методом контурных токов;

б) методом узловых потенциалов.

2) Проверить правильность расчёта токов по балансу электрических мощностей.

3) Построить потенциальную диаграмму для контура  a-b-c-d-e-a.

4) Методом эквивалентного генератора рассчитать токи в ветви, содержащей источник ЭДС Е2.

5) Методом наложения с использованием преобразований электрической цепи найти ток в ветви с резистором R4.

6) Составить сводную таблицу результатов расчета.

                     Параметры цепи (исходные данные)

Примечание: Внутреннее сопротивление источника ЭДС Е2 равно нулю.

                                     Схема цепи

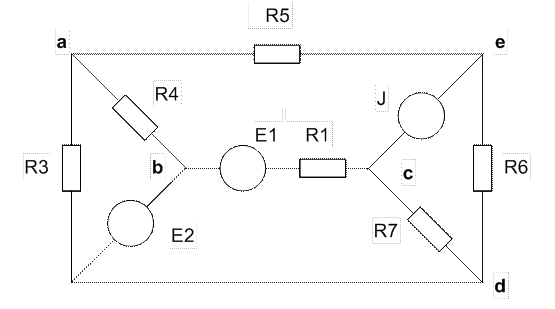
     1. Рассчитаем заданную электрическую цепь методом контурных токов. Для этого проставим направления токов в ветвях цепи и произвольно зададим положительные направления контурных токов для каждого независимого контура электрической схемы (так, чтобы каждый из них проходил через один источник тока в направлении, совпадающем с направлением тока источника).Рис. 1

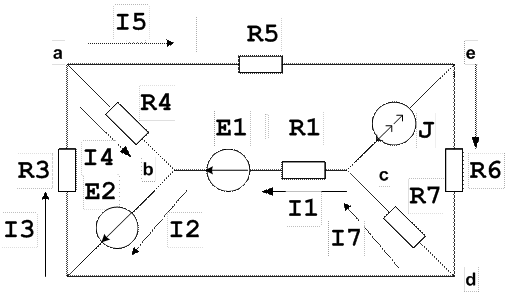
                                     Рис. 1

  Выберем направления контурных токов

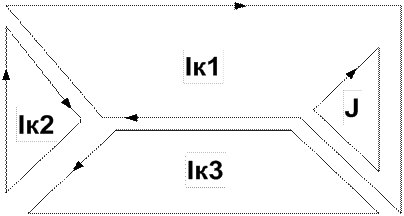
                                      Рис. 2

        Составляем систему уравнений следующего вида

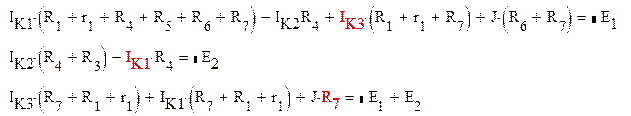
         Подставим известные величины в  данную систему и найдём корни уравнений

(составим матрицу и найдем корни при помощи метода Крамера)

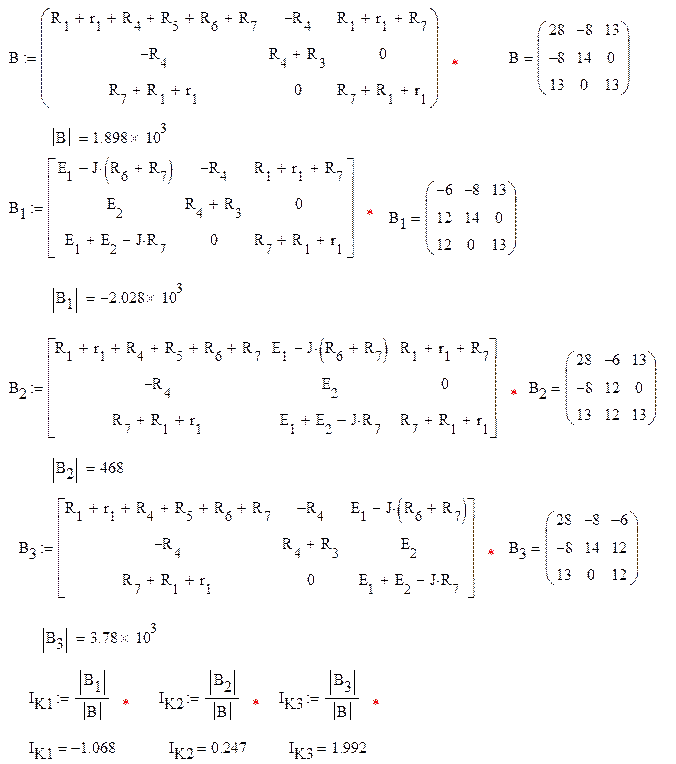
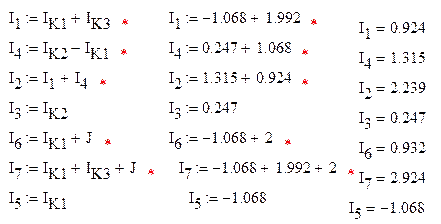
Ток I.5 направлен противоположно выбранному на схеме

       2.Рассчитаем данную схему по методу узловых потенциалов. Для этого примем потенциал узла b равным 0 и найдем проводимости ветвей

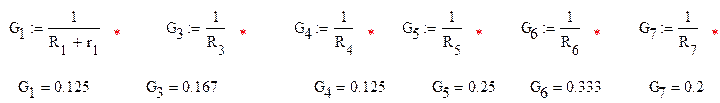
Составим систему и решим её при помощи метода Крамера относительно потенциалов узлов

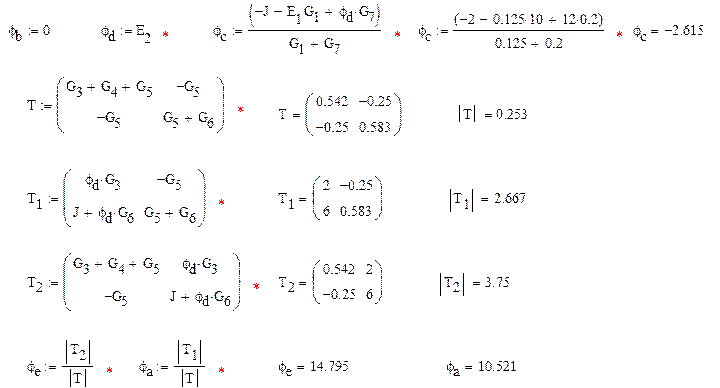
Из закона Ома найдем токи циркулирующие в ветвях

       3.Проверим правильность проведенных расчетов по балансу электрических мощностей, для этого найдем мощность, выделяющуюся в сопротивлениях при прохождении по ним электрического тока, и сравним её с мощностью источников тока и ЭДС.

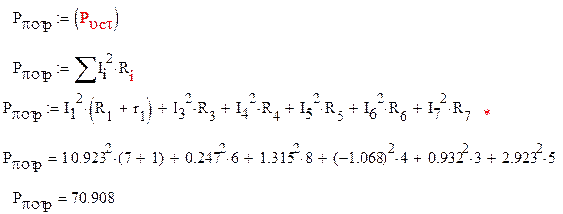
Из второго закона Киргофа запишем

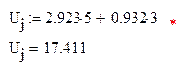
Тогда

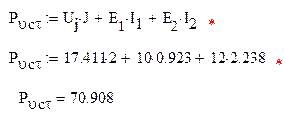
Допустимое расхождение в балансе мощностей не превышает 1%

4.Построим потенциальную диаграмму для контура a-b-c-d-e-a.Для этого потенциалы узлов возьмем из метода узловых потенциалов, предварительно рассчитав потенциал промежуточного узла между источником ЭДС и сопротивлением R1.

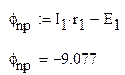
Проверим правильность расчета найдя потенциал узла b при помощи закона Ома

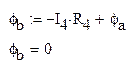
Таким образом имеем

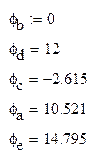
5.При помощи метода наложения с использованием преобразований электрической цепи найдем ток в ветви с резистором R4

5.1.Преобразуем схему, оставив в ней только источник ЭДС Е1, и найдем для нее ток в ветви с источником сопротивления R4

                                        Рис. 3

Но при действии источника ЭДС Е1 ветвь с сопротивлением R4 шунтируется, так что ток в ней равен 0.

5.2. Преобразуем схему, оставив в ней только источник ЭДС Е2, и найдем для нее ток в ветви с источником сопротивления R4

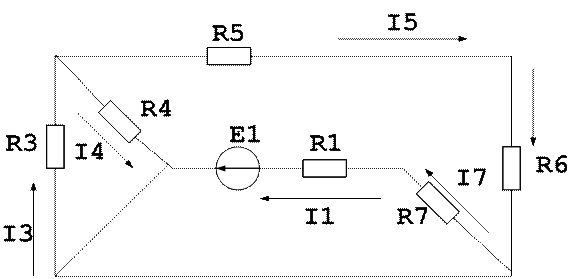
                                    Рис. 4

Для облегчения расчетов полученную схему приведем к следующему виду

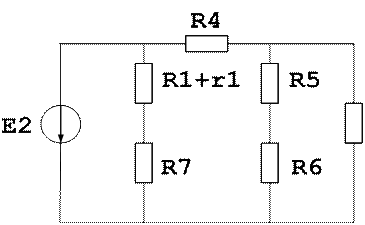
                                  Рис. 5

Произведем расчеты для полученной схемы

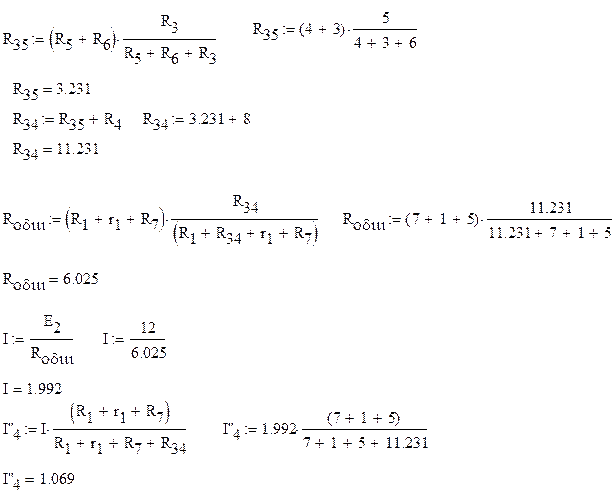
5.3. . Преобразуем схему, оставив в ней только источник тока J, и найдем для нее ток в ветви с источником сопротивления R4

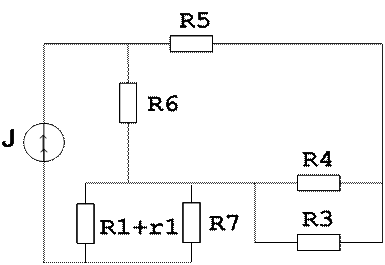
                           Рис. 6

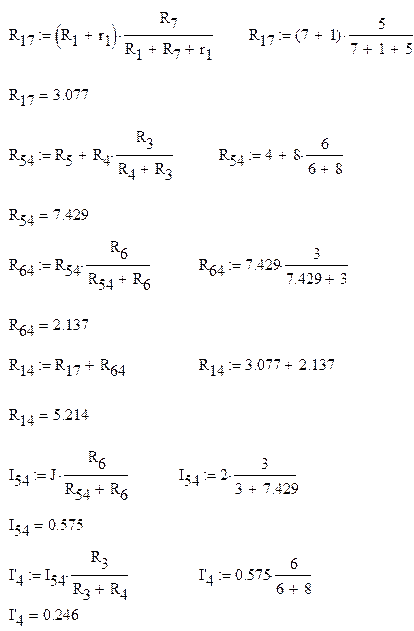
5.4.Найдем сумму частичных токов, которая в итоге и даст ток I4

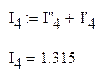
6.Методом эквивалентного генератора рассчитаем ток(I2) в ветви, содержащей источник ЭДС Е2, для этого отсоединим ветвь, ток в которой требуется найти, и найдем напряжение    между разомкнутыми разъемами при помощи метода узловых потенциалов дл полученной схемы

                                        Рис. 7

Определим контура и проставим направления контурных токов для данной цепи

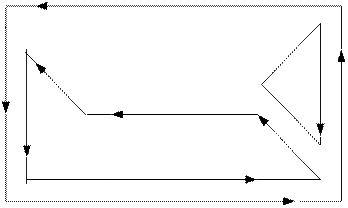
                                 Рис. 8

Составим  систему уравнений относительно контурных токов для данной схемы

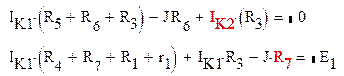
Решим полученную систему уравнений при помощи метода Крамера

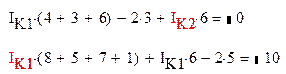
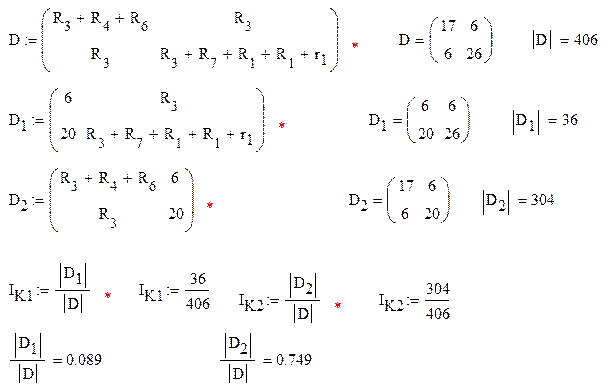
Тогда

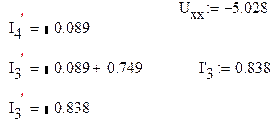
Для контура, содержащего сопротивления R3 и R4 и напряжение холостого хода составим уравнение по второму закону Киргофа

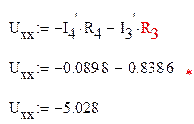
Найдем сопротивление цепи относительно разомкнутых зажимов, для этого приведем нашу схему к следующему виду

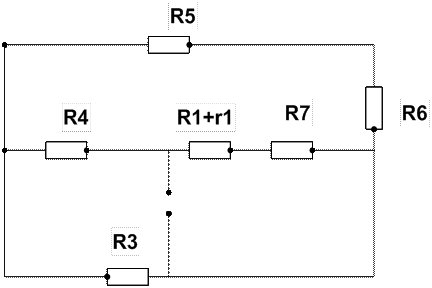
                                 Рис.9

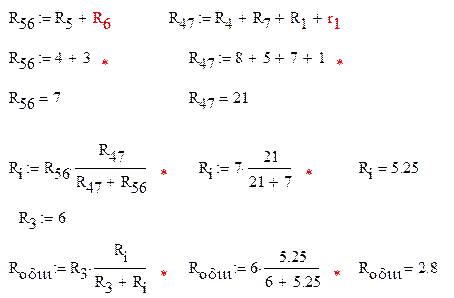
Найденные значения и U.xx представляют собой параметры

эквивалентного генератора напряжения соответственно

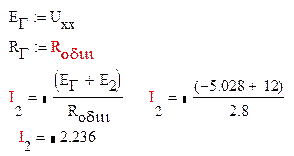
Составляем сводную таблицу результатов расчета