





Расчет электростатического поля несоосных
параллельных цилиндров
1. Для заданной системы двух параллельных цилиндров , имеющих равные заряды противоположного знака (q1 = - q2 ) определить :
a) емкость ;
b) напряжение.
При этом поле считать плоскопараллельным.
2.Построить графическую картину электростатического поля , соблю-
дая следующие требования :
a) разность потенциалов между двумя любыми соседними линиями
равного потенциала должна быть одна и та же ;
b)поток вектора напряженности электростатического поля во всех
силовых трубках должен быть одинаков ;
с)при построении картины поля на каждой линии равного потенциа-
ла указать значение потенциала ; на силовых линиях должно быть
указано их направление и ограниченное данной линией значение по-
тока напряженности поля, отсчитываемое от некоторой фиксирован- ной линии , принятой за начальную.
3.Вычертить и представить в виде графиков изменение потенциала и
напряженности электростатического поля на линии, соединяющей
наиболее близкие точки цилиндров, и распределение плотности заряда
на поверхности цилиндра меньшего радиуса.
er = 1.5 ; l = 15 м ; q = 13 мкКл ; R1 = 26 см ; R2 = 12 см ; D = 64 см ;
Знак заряда (минус).
Примечание
Знак заряда относится к цилиндру меньшего радиуса.
1.Для заданной системы двух параллельных цилиндров, имею- щих равные заряды противоположного знака (q1 = - q2 ) определим :
a)емкость ;
b)напряжение.
Считаем цилиндры бесконечно длинными, а поле, создаваемое ими – плоскопараллельным.
Заменим цилиндры заряженными нитями с линейными зарядами :
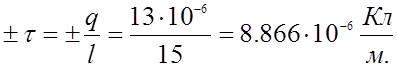 |
потенциала.
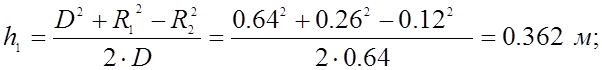 |
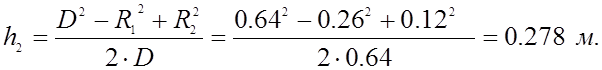 |
Определим расстояние от плоскости нулевого потенциала до
мнимых заряженных осей.
Определим напряжение между цилиндрами, как разность потен-
циалов между точками A и B.
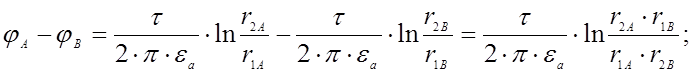
где
Откуда получаем, что
Емкость найдем из выражения :
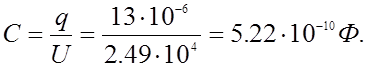 |
2.Построим графическую картину электростатического поля , соблюдая следующие требования :
a)разность потенциалов между двумя любыми соседними линиями
равного потенциала должна быть одна и та же ;
b)поток вектора напряженности электростатического поля во всех
силовых трубках должен быть одинаков ;
с)при построении картины поля на каждой линии равного потенциа-
ла указать значение потенциала ; на силовых линиях должно быть
указано их направление и ограниченное данной линией значение по-
тока напряженности поля, отсчитываемое от некоторой фиксирован- ной линии , принятой за начальную.
Построим эквипотенциальные линии.
Линии равного потенциала есть окружности сцентрами, лежащи-ми на линии, соединяющей оси цилиндров.
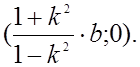 |
Радисы находим из выражения:
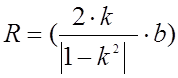 |
постоянной, необходимо, что бы выполнялось следующее условие:
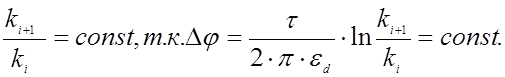 |
Примем
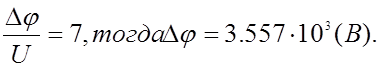 |
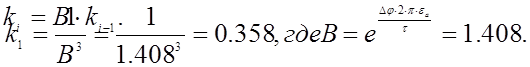 |
тогда плучаем, что эквипотенциальные линии будут иметь окружности
радиусами R с координатами (x;0).
|
k |
j,В |
X,м |
R,м |
|
|
1 |
0.358 |
-10920.1 |
0.3248 |
0.206 |
|
2 |
0.504 |
-7283.9 |
0.4224 |
0.3396 |
|
3 |
0.71 |
-3640.91 |
0.7613 |
0.7186 |
|
4 |
0.999 |
-10.6 |
353.12 |
353.12 |
|
5 |
1.407 |
3629.96 |
-0.7642 |
0.7217 |
|
6 |
1.981 |
7267.17 |
-0.4231 |
0.3404 |
|
7 |
2.789 |
10903.7 |
-0.3254 |
0.2067 |
Построим силовые линии
Силовые линии поля двух параллельных заряженных нитей пред-
ставляет собой окружности с координатами центров :
![]()
угол, под которым расстояние между нитями видно
из любой точки
линии.
Так как
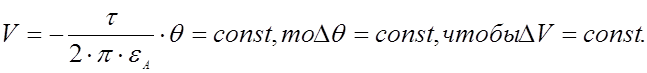
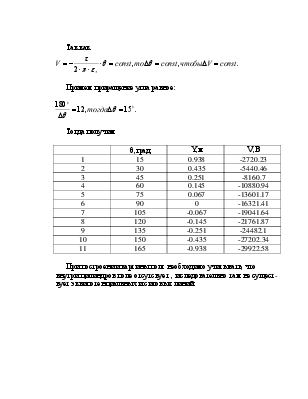
Примем приращение угла равное:
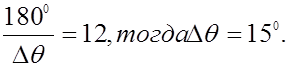
Тогда получим
|
q,град |
Y,м |
V,В |
|
|
1 |
15 |
0.938 |
-2720.23 |
|
2 |
30 |
0.435 |
-5440.46 |
|
3 |
45 |
0.251 |
-8160.7 |
|
4 |
60 |
0.145 |
-10880.94 |
|
5 |
75 |
0.067 |
-13601.17 |
|
6 |
90 |
0 |
-16321.41 |
|
7 |
105 |
-0.067 |
-19041.64 |
|
8 |
120 |
-0.145 |
-21761.87 |
|
9 |
135 |
-0.251 |
-24482.1 |
|
10 |
150 |
-0.435 |
-27202.34 |
|
11 |
165 |
-0.938 |
-29922.58 |
При построении картины поля необходимо учитывать, что внутри цилиндров поле отсутсвует , и следовательно там не сущест-
вует эквипотенциальных и силовых линий.
3. Вычертим и представим в виде графиков изменение потенциала и
напряженности электростатического поля на линии, соединяющей
наиболее близкие точки цилиндров, и распределение плотности заряда
на поверхности цилиндра меньшего радиуса.
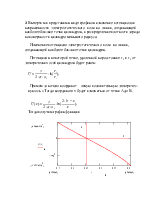
Изменение потенциала электростатического поля на линии, соединяющей наиболее близкие точки цилиндров.
Потенциал в некоторой точке, удаленной на расстояние r1 и r1 от
электрических осей цилиндров будет равен:
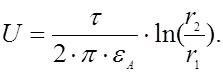 |
Примем за начало координат – левую положительную электричес- кую ось t.Тогда координата x будет изменяться от точки А до В.
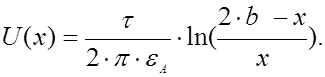 |
Тогда получим график функции
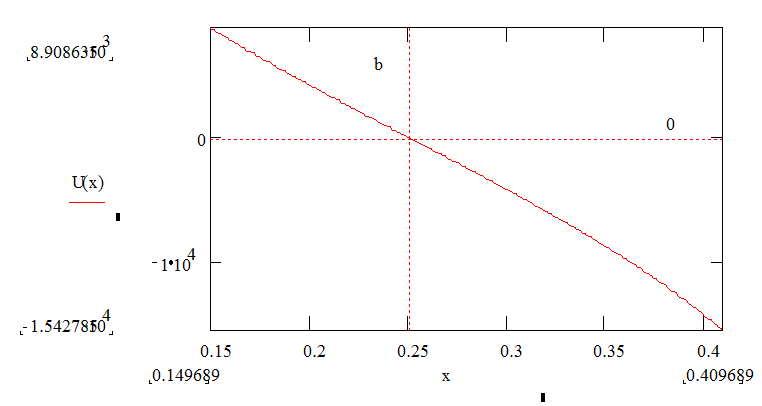 |
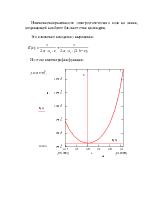
Изменение напряженности электростатического поля на линии, соединяющей наиболее близкие точки цилиндров.
Это изменение находим из выражения:
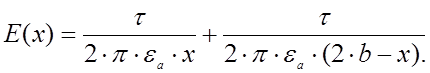 |
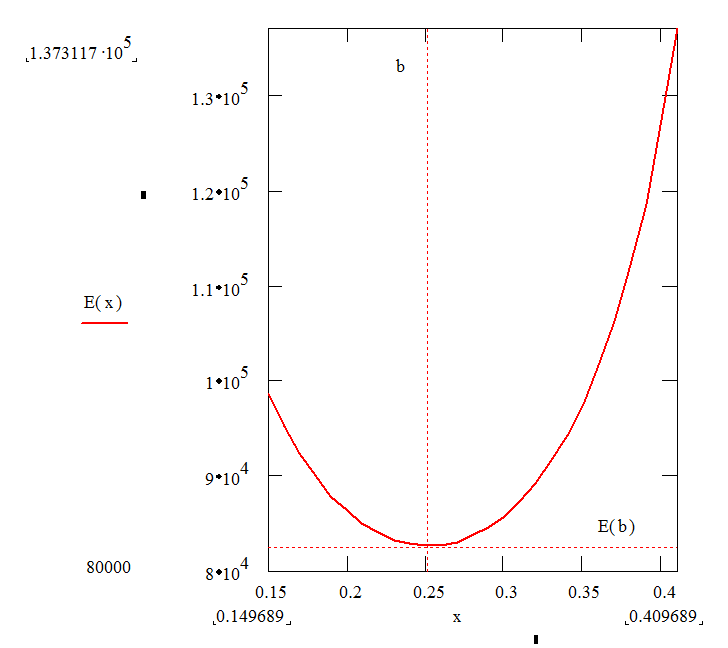
Из этого имеем график функции:
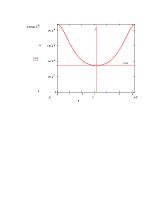
Исходя из граничных условий на поверхности раздела проводника
и диэлектрика имеем, что
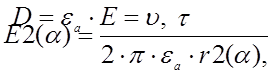
где u - плотность
электрического заряда на поверхности цилиндра.
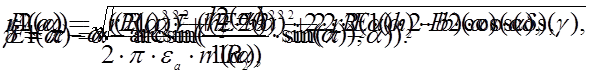
Получим график
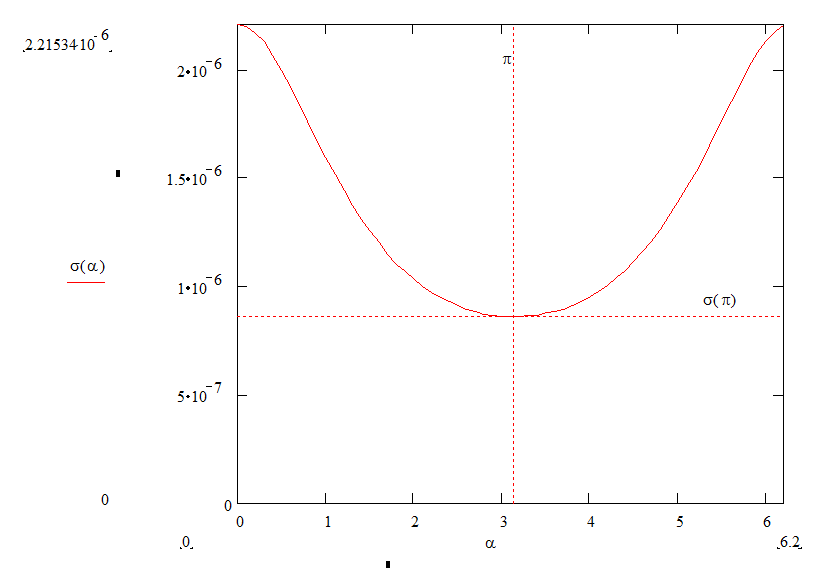
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.