Расчет токов во всех ветвях и напряжения на реактивных элементах электрической цепи

Задача 1.  Для схемы, изображенной на рисунке требуется:

1. Классическим методом рассчитать токи во всех ветвях и напряжения на реактивных элементах.
2. Операторным методом рассчитать ток в катушке индуктивности или напряжение на конденсаторе.
3. Построить график изменения напряжения на конденсаторе.

Исходные данные: L = 30 мГн,    С = 50 мкФ,   R = 8 Ом,   E = 24 В

Схема электрической цепи

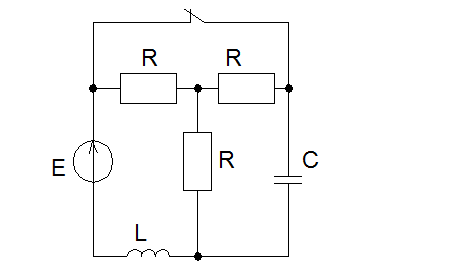
Решение:

1. Расчет классическим методом.

После размыкания рубильника схема будет иметь следующий вид:

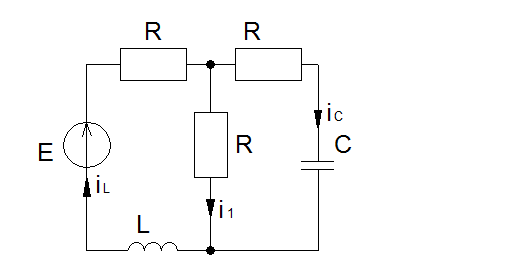
Для данной схемы, исходя из законов Кирхгофа, запишем систему уравнений:

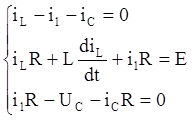      (*)                  где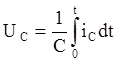

Получим  систему алгебраических уравнений для свободных составляющих переходных токов:

заменяем дифференцирование умножением на p, интегрирование – делением на p:

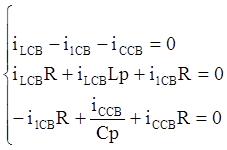
Решение этой системы будет нетривиальным, если определитель   данной системы будет равняться нулю.

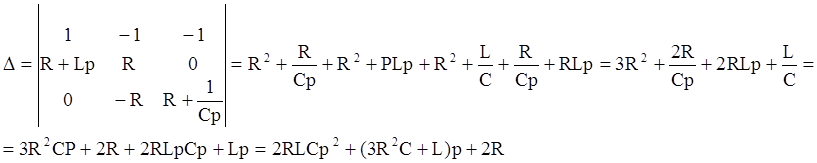
После подстановки соответствующих значений для RLC, получим следующее квадратное уравнение:

Найдем корни этого уравнения:

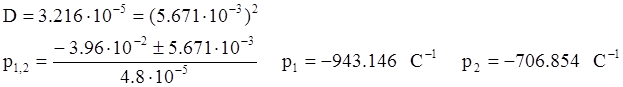
Из расчетов видно, что корни характеристического уравнения действительные, причем ,

следовательно, переходной процесс носит апериодический характер.

В данном случае ток в индуктивности и напряжение на емкости определяются следующим образом:

   (**)

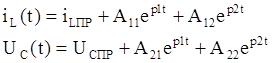Определим принужденные составляющие:

Рассмотрим послекоммутационную схему:

 

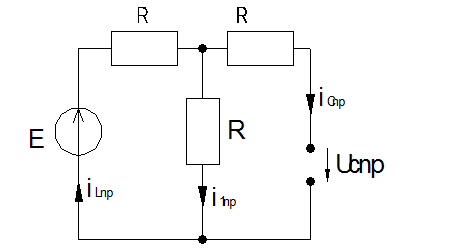
В этой цепи индуктивность закорочена,

ветвь с емкостью разорвана.

Из схемы видно, что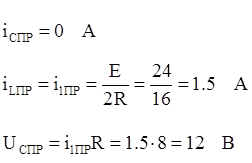

Найдем независимые начальные условия:

Рассмотрим докоммутационную схему:

 

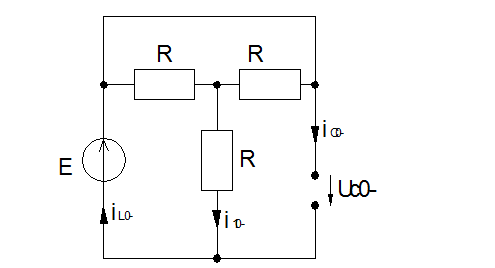
В этой цепи индуктивность закорочена,

ветвь с емкостью разорвана.

Напряжение на емкости определяется напряжением источника ЭДС:

Ток в цепи определяется следующим образом:

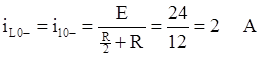
По законам коммутации получаем выражения для момента размыкания:

Значение для получим исходя из 1-го и 3-го уравнений системы (*):

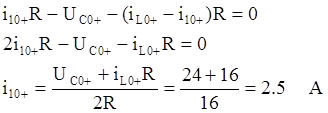
 определяется из 1-го уравнения системы (*):

Определим зависимые начальные условия:

Из 2-го уравнения системы (*) следует: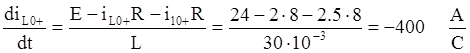

Так как 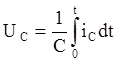, то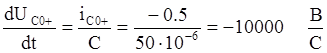  

Рассмотрим уравнения (**) при t = 0:

Подставляя значения для  и  в эти выражения получим:

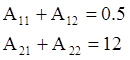
Продифференцируем уравнения (**), принимая t = 0 :

Подставляя значения для производных и для , получим следующие соотношения:

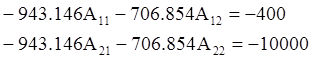
Таким образом получаем системы уравнений для нахождения постоянных интегрирования:

                       

                      

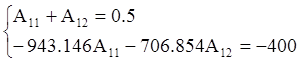
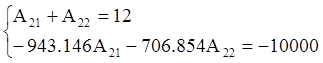
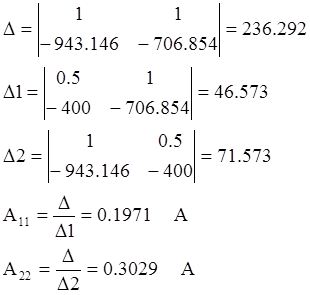
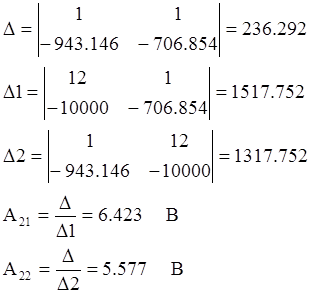
Подставляя найденные значения для постоянных интегрирования в уравнения (**), получим:

Найдем напряжение на катушке:

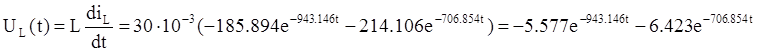 В

Исходя из 2-го уравнения системы (*) следует, что: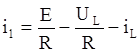

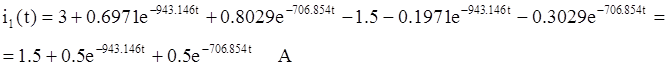
Исходя из 3-го уравнения системы (*) следует, что: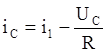

 А

Таким образом, мы получили следующие зависимости:

  А

 В

Проверим правильность расчета по 1-му закону Кирхгофа:

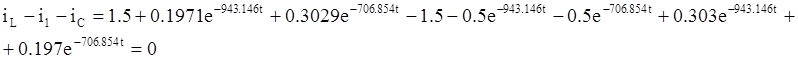
Следовательно, расчет правильный.

2. Расчет операторным методом.

Найдем независимые начальные условия:

Рассмотрим докоммутационную схему:

 

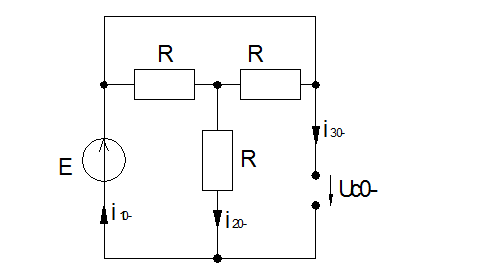
В этой цепи индуктивность закорочена,

ветвь с емкостью разорвана.

Напряжение на емкости определяется напряжением источника ЭДС:

Ток в цепи определяется следующим образом:

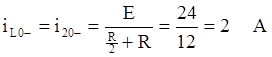
По законам коммутации получаем выражения для момента размыкания:

Рассмотрим операторную схему замещения:

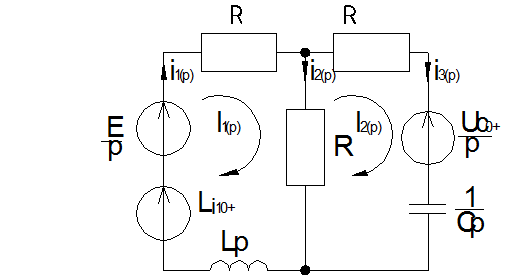
Для определения изображения тока в катушке индуктивности () применим метод контурных токов.

При данном разбиении на контуры изображение тока в катушке индуктивности будет равен току 1-го контура:

Система уравнений по методу контурных токов имеет вид:

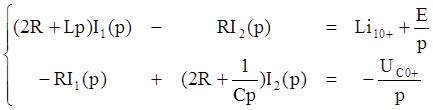
Найдем по методу Крамера:

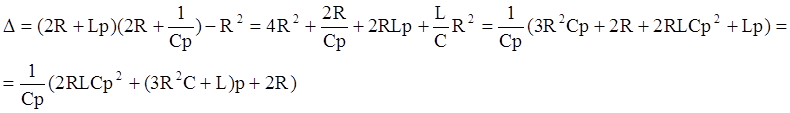
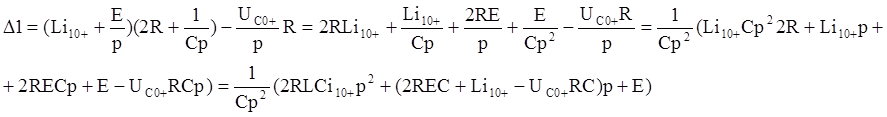
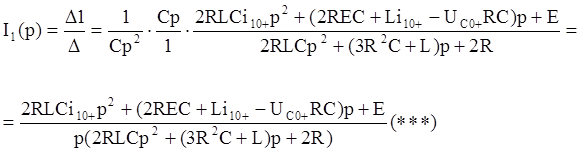
Подставив значения для  в , получим следующее выражение:

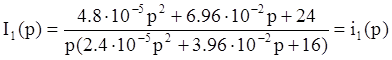
Определим корни знаменателя:

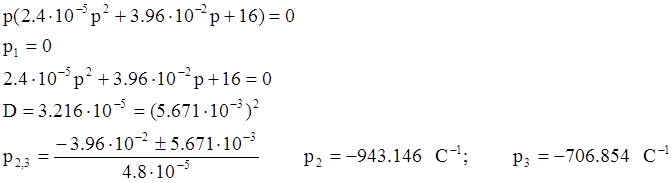
Используя теорему разложения, найдем оригинал тока :

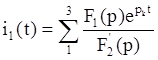
В нашем случае: ; 

                              

Таким образом:

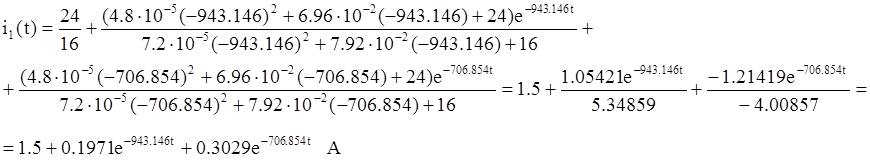
Расчет классическим методом дал тот же результат, следовательно, расчет правильный.

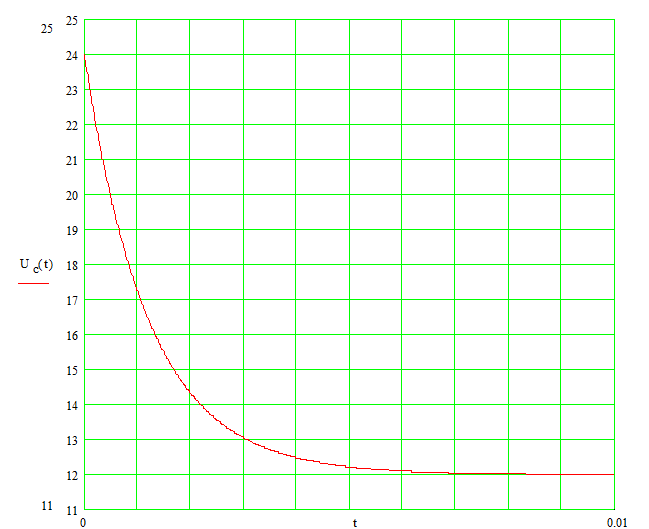
График изменения напряжения на конденсаторе:

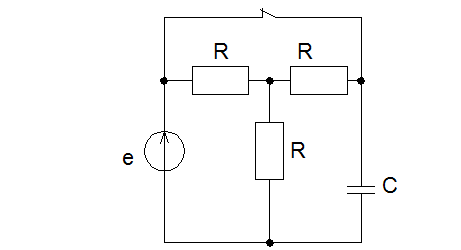
Задача 2.  Для схемы, изображенной на рисунке требуется:

1.  Определить закон изменения напряжения на конденсаторе.

Исходные данные:  С = 50 мкФ,   R = 8 Ом,   Em = 36 В, f=30^o , 

                                 

Схема электрической цепи

Решение:

Найдем независимые начальные условия:

Рассмотрим докоммутационную схему:

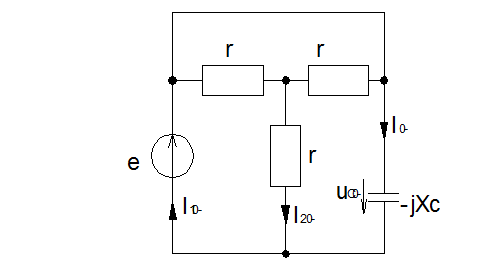
Исходя из схемы видно, что напряжение на конденсаторе равно напряжению источника синусоидальной ЭДС:

По закону коммутации:

Так как коммутация происходит в момент

времени t = 0, то

Определим принужденные составляющие:

Рассмотрим послекоммутационную схему:

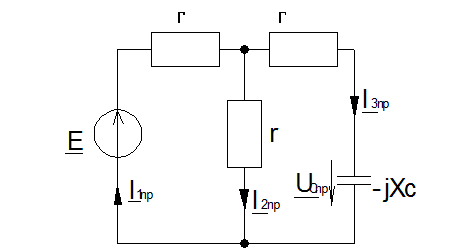
Здесь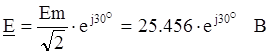

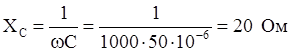
Найдем эквивалентное сопротивление относительно источника ЭДС:

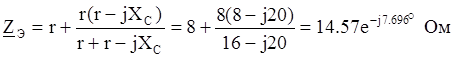
По закону Ома принужденный ток в 1-ой ветви равен:

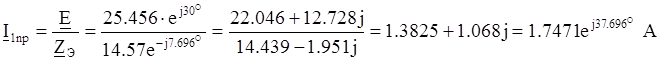
По правилу разброса токов найдем принужденный ток в 3-ей ветви:

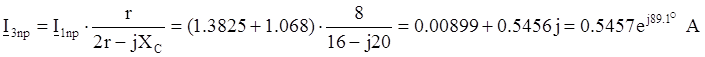
Найдем принужденное напряжение на конденсаторе:

Или

После размыкания рубильника схема будет иметь следующий вид:

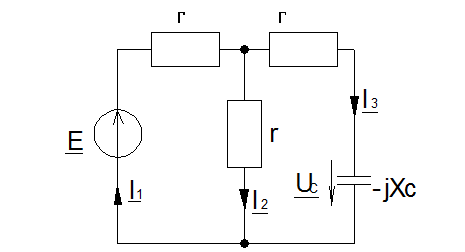
По законам Кирхгофа можно записать:

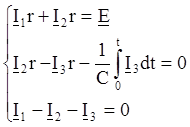
Получим  систему алгебраических уравнений для свободных составляющих переходных токов: заменяем дифференцирование умножением на p, интегрирование – делением на p:

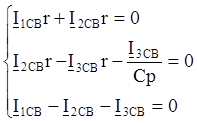
Решение этой системы будет нетривиальным, если определитель   данной системы будет равняться нулю.

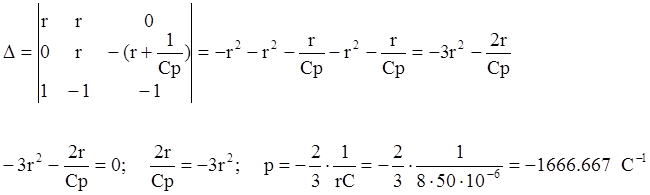
Таким образом, свободная составляющая напряжения на конденсаторе имеет вид:

 В

Переходное напряжение определяется по формуле:

В момент времени t = 0  , следовательно:

откуда

Значит: