Задача 2. Расчёт линейной электрической цепи с несинусоидальными источниками напряжения.
К электрической цепи приложено напряжение U(t), заданное графически в виде периодической несинусоидальной функции.
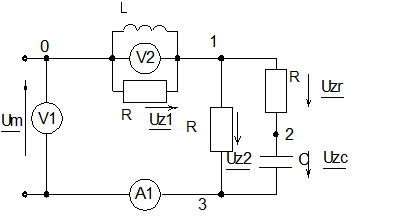
Исходные данные: L = 0.02 Гн, С = 40 мкФ, R = 22 Ом, Ua(t) = 100 В, w = 800 с-1
График U(t)
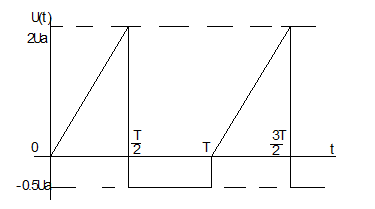
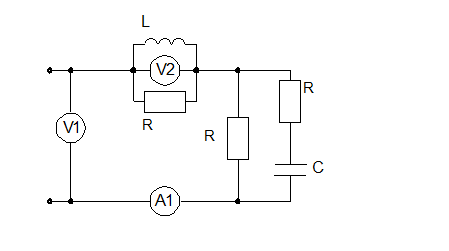
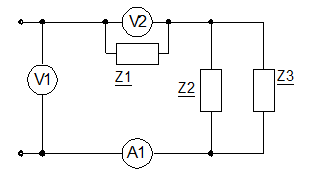
Схема электрической цепи
Решение:
Аналитическое выражение функции U(t), исходя из графика, следующее:
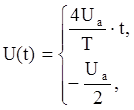
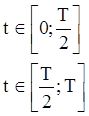
Для разложения функции U(t) в ряд Фурье найдём коэффициенты A0, Вkm, и Ckm:
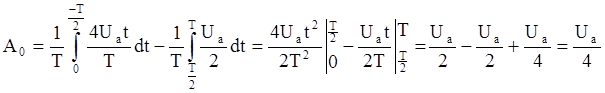
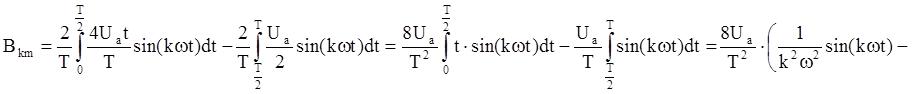
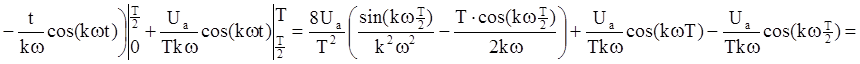
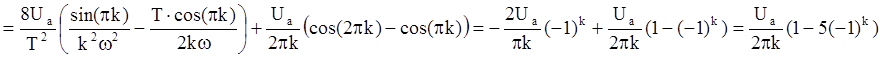
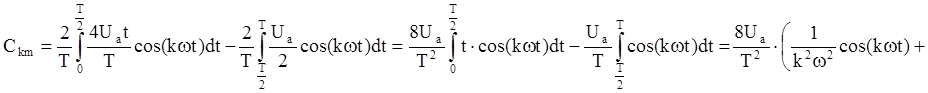
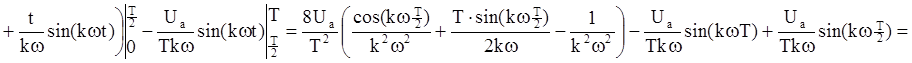
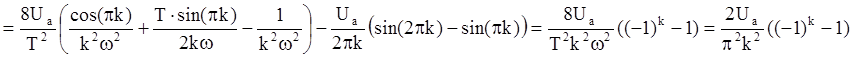
Учитывая, что Ua=100 В,
то ![]() ,
, 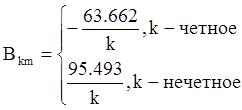 ,
, 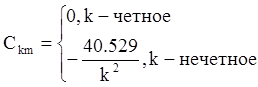
![]()
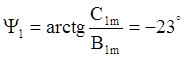
![]()
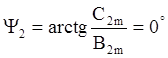
![]()
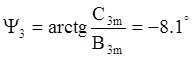
Таким образом, ряд Фурье до третьей гармоники имеет вид:
![]() В.
В.
Произведем расчет параметров схемы:
Параллельные катушку L и резистор R в ветви 1 заменим сопротивлением ![]() .
.
Резистор R в ветви 2 заменим на
сопротивление ![]() .
.
Резистор R в ветви 3 заменим на
сопротивление ![]() .
.
Сопротивление ветви 3 равно ![]() ,
сопротивление параллельных ветвей 2 и 3 равно
,
сопротивление параллельных ветвей 2 и 3 равно ![]() .
.
Соответствующие сопротивления для k-ой гармоники равны:
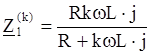
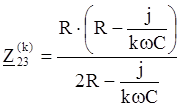
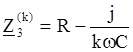
![]()
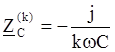
![]()
Найдём токи в ветвях 1, 2, 3 для k-ой гармоники:
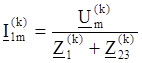
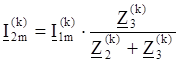
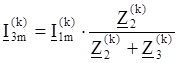
Найдём падения напряжения на элементах схемы для k-ой гармоники:
![]()
![]()
![]()
![]()
Показания измерительных приборов для k-ой гармоники имеют следующие выражения:
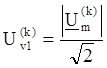
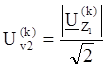
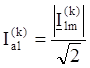
Найдём активную и пассивную мощности для k-ой гармоники:
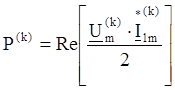
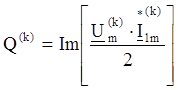
Подставляя номер гармоники в вышеуказанные выражения получаем следующие значения:
Постоянная составляющая:
![]() Ом
Ом
![]() Ом
Ом
![]() В
В
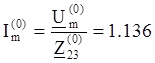 А
А
![]() А
А
![]() В
В
![]() В
В
![]() Вт
Вт ![]() см
см
Значения для трёх первых гармоник сведём в таблицу:
|
Первая гармоника |
Вторая гармоника |
Третья гармоника |
|||
|
|
Ом |
|
Ом |
|
Ом |
|
|
Ом |
|
Ом |
|
Ом |
|
|
Ом |
|
Ом |
|
Ом |
|
|
Ом |
|
Ом |
|
Ом |
|
|
Ом |
|
Ом |
|
Ом |
|
|
Ом |
|
Ом |
|
Ом |
|
|
В |
|
В |
|
В |
|
|
А |
|
А |
|
А |
|
|
А |
|
В |
|
А |
|
|
А |
|
В |
|
А |
|
|
В |
|
В |
|
В |
|
|
В |
|
А |
|
В |
|
|
В |
|
Вт |
|
В |
|
|
В |
|
См |
|
В |
|
|
В |
|
В |
||
|
|
В |
|
В |
||
|
|
А |
|
А |
||
|
|
Вт |
|
Вт |
||
|
|
см |
|
см |
||
Показания приборов имеют следующие значения:
![]() А
А
![]() В
В
![]() В
В
Найдём активную и реактивную мощности:
![]() Вт
Вт
![]() см
см
Полная мощность цепи равна:
![]() ВА
ВА
![]()
![]() =>
расчёт правильный
=>
расчёт правильный
Выражения для входного тока имеет следующий вид:
![]() А
А
График зависимости U(t):
U(t)-результат сложения гармоник, U0(t)-U3(t) – гармонические составляющие, U00(t)-исходный график.
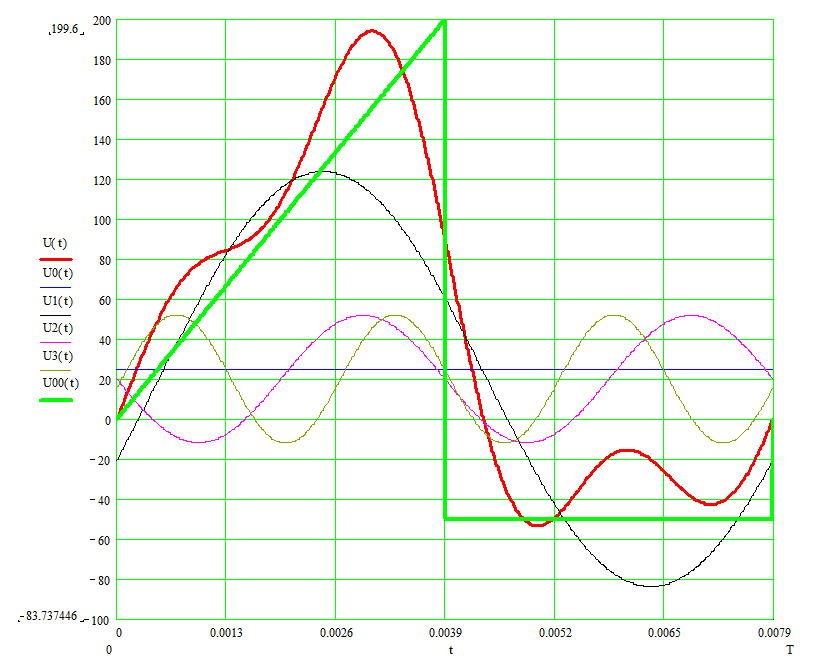
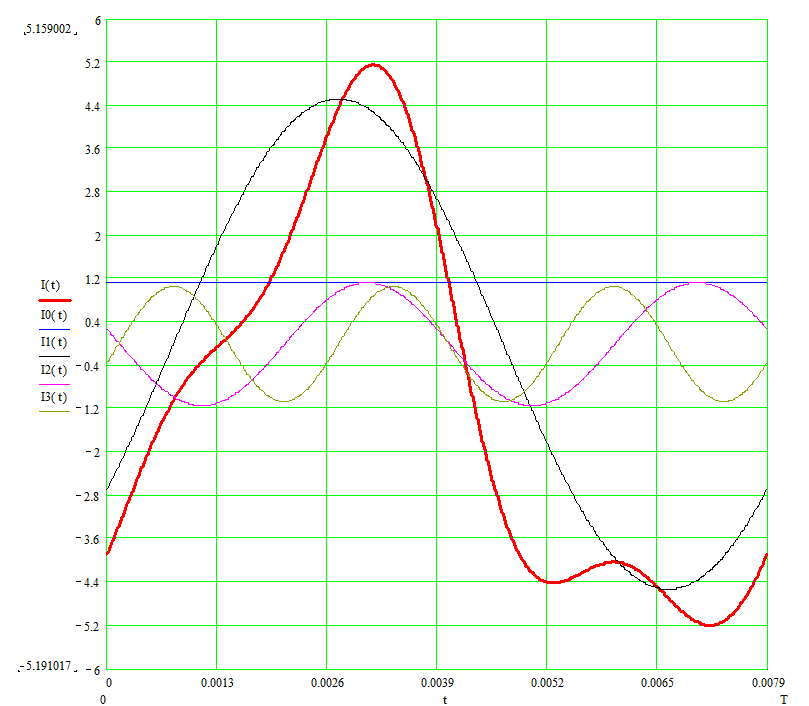
График зависимости I(t):
I(t)-результат сложения гармоник, I0(t)-I3(t) – гармонические составляющие.
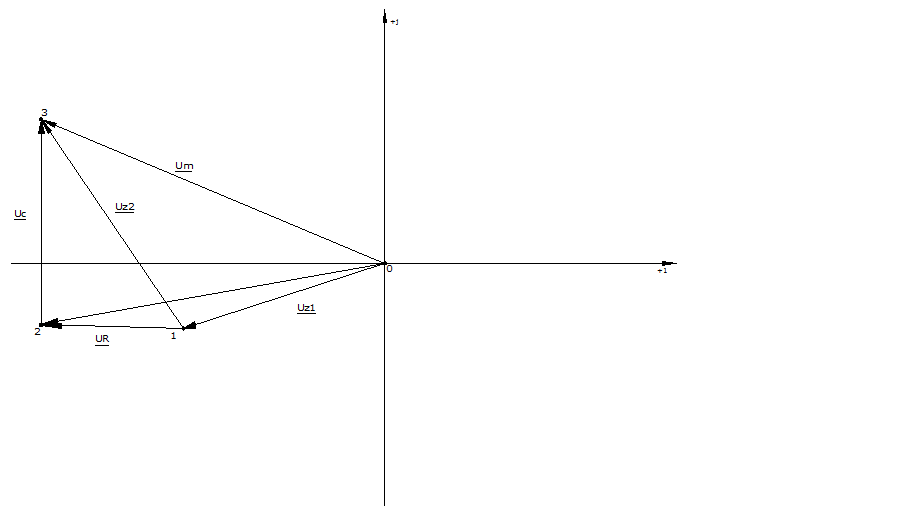
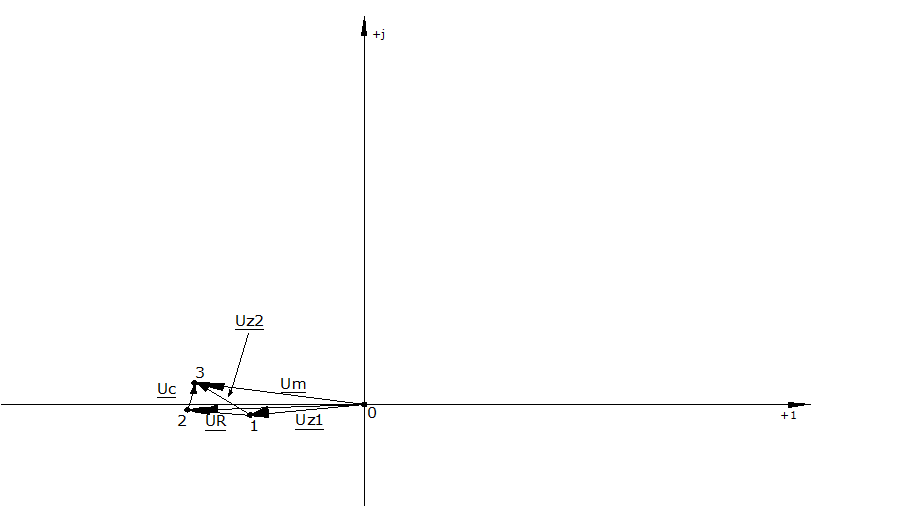
Для построения топографической диаграммы найдем потенциалы точек 1,2,3, принимая потенциал точки 0 равным нулю:
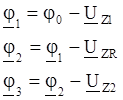
Для первой гармоники: 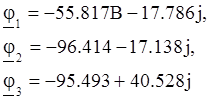
![]() строим в масштабе 1:1
строим в масштабе 1:1
Для второй гармоники: 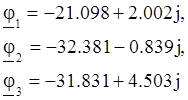
![]() строим в масштабе 1,188
строим в масштабе 1,188![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.