Другие предметы \ Теория передачи сигналов

Показатели качества систем передачи информации. Основные модели и статистические характеристики помех в кана­лах передачи. Демодулятор и модуляторы АМ сигналов. Преимущества и недостатки цифровых систем передачи, страница 4

При интерполяции алгебраическими полиномами интерполирующая функция

Для того чтобы найти коэффициенты akмногочлена (2.37), необхо­димо составить и совместно решить систему из (N+ 1) уравнений вида

где k = О, I, 2, ..., N.

Соответственно при использовании полинома Лагранжа нулевой (А/ = 0), первой (N = 1) и второй (N = 2) степеней различают ступен­чатую, линейную и квадратичную интерполяции.

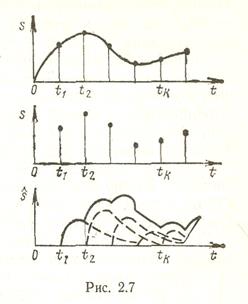
Наиболее простым видом интерполяции, при которой использует­ся алгебраический полином нулевой степени, является ступенча­тая интерполяция. Как показывает само название, при сту­пенчатой интерполяции непрерывная функция s (t) заменяется ступен-

 


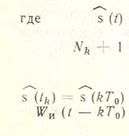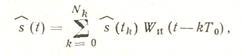
9.Числовыехарактеристики случайных непрерывных сигналов.

Мат. ожиданием называется ср.значение случайного сигнала определяемое из выражения

 


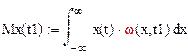мат.ожидание является функцией времени т.е. не случайной величиной. Дисперсией случайного сигнала наз. фун-я значение которой для каждого аргумента времени t равно дисперсии соответствующего значения случайного сигнала

дисперсия случайного сигнала показ. разбросанность его значений относительно ср.значения. Корреляционные функции означают ср.значение и дисперсия случайного сигнала не полностью хар-т этот процесс т.к. не определена динамика изменения случайного сигнала. Для определения динамич.свойств изменения сигналов т.е. оценки изменения в различных точках времени применяется ф-я корреляции, а так же автокорреляции. Корреляционная ф-я показывает степень взаимной зависимости м-у значениями одного случайного сигнала в различных точках временной оси (показывает только линейную зависимость

10. К основным параметрам дискретн источника информации относятся:

1. Алфавит источника информации   А   при   а  не = 0

               а1,а2,…ак              -знак алфавита                               

     А =  р1,р2,…рк       -вероятность появл на входе ист.                                                                     

      å Р(ак)=1

2. Энтропия представляет собой количество информации содержащейся в среднем в одном знаке сообщения с единицей   

3.скорость передачи (единичн. элементов)-В;

энтропия, т.е. количество информации, содержащейся в среднем в одном знаке сообщения,-Н с единицей измерения бит на символ.

4.поток информации характеризует информацию поступающую от источника за единицу времени

                                                I(g)=H(g)/tср  

tср- среднее время передачи одного сообщения

                         tср=å ti p(gi)

ti-длительность i-го сообщ.

5.Кооф. избыточности источника сообщения:

                       Кизб=1- H(g)/Hmax

Hmax-максимально возможная энтропия источника сообщен. Если его символы были независимы и равновероятными

18.Оптимальный приём сигналов. Алгоритм принятия решения по сообщению.

Предположим, что на вход приёмника поступа-

ет адитивная смесь полезного сигнала, передав.

по каналу связи, и напр- ие шума

y(t)=Ul(t)+Uш(t)

Приём. устр-во осущ-ет выделение сигнала из

помех и преобр-ие сигнала в сообщение. Из-за

действия помех сооб-ие на выходе будет иска-

жённым. Считается, что Ul(t) явл. непол-

ностью известным. Известно только то сооб-ие, кот. поступило на вход приёмника, т. е. y(t).

Известна также модель передав-го сигнала, т. е. вид преобразования в сигнал по цепочке

li--Uli=Ul(t)

 li-- сигнал

 Uli -- напряжение

 Ul(t)-- напр-ие на входе приёмника.

Известна, в общем случае, модель помехи, в

качестве кот. принимается «белый» шум со

спектр. плотностью помехи.

Считается известным и некоторый избранный

критерий оптим-ти. Т.к. приём сигналов проис-

ходит под действием помех, а время анализа,

конечно, ограничено, то любой приёмник не

сможет точно принять сообщение.

Самое большое, что можно требовать от приём-

ника --- это указатель вер-ти получения сооб-ия, поступившего на вход с-мы связи при дан-


ной реализации смеси, пост-го на вход приём-

Скачать файл