Показатели качества систем передачи информации. Основные модели и статистические характеристики помех в кана­лах передачи. Демодулятор и модуляторы АМ сигналов. Преимущества и недостатки цифровых систем передачи, страница 3

7. Представление непрерывных сигналов выборками и интерполяция.

При дискретизации выборками в качестве координат сигнала (со­общения) используются текущие (мгновенные) значения сигнала в фиксированные моменты времени, Коорди­наты s_fe = s (4) обычно называют выборками, или отсчета-м и, моменты времени t_ltt₂, ..., t_k — точками опроса, а сам процесс формирования таких координат — опросом ..

Мгновенные выборки могут быть представлены в виде дельта-функ­ций 8 (t_h), площадь которых равна амплитуде выборки s (/_ft) в момент отсчета. Импульсный элемент, на выходе которого имеют место дельта-функции, называют идеальным.

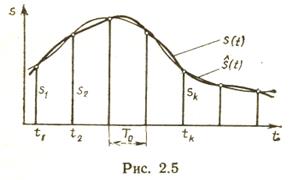
Широкое использование дискретного регулярного представления по выборкам объясняется чрезвычайной простотой его аппаратурной реализации (с использованием электронных схем, работающих в клю­чевом режиме) и достаточно высокой эффективностью.

С необходимостью дискретного представления выборками встре­чаемся прежде всего при передаче непрерывных сообщений по импульс­ным и цифровым системам передачи а также при цифро­вой обработке сигналов. Здесь основное внимание будет уделено диск­ретизации непрерывных сообщений, т. е. когда s (t) = К (t).

Последовательность дельта-выборок можно представить так

 (2.32)

где    б (/) — дельта-функция.

При передаче непрерывных сообщений импульсными методами всегда встает вопрос не только о дискретном представлении таких со­общений на передающей стороне выборками, но и об его восстановле­нии на приемной стороне по переданным дискретным значениям (вы­боркам). Этот процесс восстановления называют интерполя­цией, или интерполяционной обработкой. Последнее понятие обыч­но используется при восстановлении по зашумленным (искаженным) выборкам.

Теорема Котельникова. Основополагающей теоремой теории диск­ретного регулярного представления по выборкам является теорема Котельникова. В соответствии с этой теоремой(врз можно со сколь угод­но высокой точностью восстановить любой непрерывный детерминиро­ванный или случайный процесс (сигнал) s (t) по его дискретным регу­лярным выборкам при следующих условиях: процесс имеет ограничен­ный спектр (например, от 0 до F_r); процесс наблюдается бесконечное время (Т->• оо); выборки сообщения формируются с частотой опроса

 (2.33)

восстановление процесса ведется по точным (незашумленным) значе­ниям выборок в форме ряда Котельникова

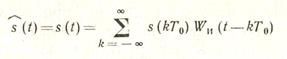 (2.34)

с помощью так называемых функций отсчета

Следует отметить, что теорема Котельникова дает лишь предельные (потенциальные) соотношения для определенных идеализированных условий, основными из которых являются ограниченность спектра и бесконечное время наблюдения. К этим предельным соотношениям можно лишь стремиться, никогда их не достигая.

Восстановление реальных непрерывных процессов s (t) с неогра­ниченным спектром по выборкам s (t_k) за конечное время наблюдения может осуществляться лишь с определенной, так называемой интер­поляционной погрешностью при использовании ря­да Котельникова и любой другой интерполяционной формулы (метода интерполяции). Причем частоту опроса р_й всегда следует выбирать су­щественно больше 2F_G. Значение интерполяционной погрешности за­висит от вида сообщений, метода интерполяции и частоты опроса F₀.

методами: операторами вручную, различными аналоговыми фильтрами.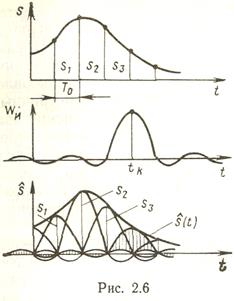  

электронной вычислительной машиной (ЭВМ), реализующей различные алгоритмы интерполяции. Вследствие простоты реализации, в том чис­ле и на ЭВМ, для восстановления непрерывных сообщений по диск­ретным выборкам широко используются алгебраические полиномы (в основном полиномы Лагранжа невысоких степеней) и сплайны.

Простейшие виды интерполяции алгебраическими полиномами.

За­дача интерполирования алгебраическими полиномами обычно формули­руется так. Если на интервале интерполирования длительностью Т = = а/то заданы N+ 1 точек опроса 0,1, 2, ..., Nи значения выборок в этих точках s (t_Q), s(^), ..., s (tv), то можно построить алгебраический полином рм (t) степени N, который будет проходить через N+ 1 за­данные точки, принимая значения s (t_k).