В большинстве случаев считается, что флуктуационная помеха (шум) является стационарным процессом и имеет постоянную спектральную плотность мощности в пределах полосы пропускания исследуемой системы, т. е. может аппроксимироваться белым шумом. Спектральная плотность мощности белого шума N0представляет собой мощность шума, выделяемую на сопротивлении 1 Ом в полосе 1 Гц и имеет размерность ватт на герц.
На выходе узкополосного тракта со средней частотой со0 флуктуационную помеху можно представить в виде колебаний
где Un (t), 9n (t) — случайные амплитуда (огибающая) и фаза флуктуацией кого колебания.
Флуктуационная помеха характеризуется законами распределения мгновенных значений, амплитуды и начальной фазы. При исследовании обычно принимается, что одномерное распределение мгновенных значений флуктуационной помехи подчиняется гауссовскому (нормальному), закону со средним значением, равным нулю, и дисперсией а„ = = N0&fa, где no — спектральная плотность мощности белого га-уссовского шума.
Импульсная помеха представляет собой регулярную или хаотическую последовательность коротких импульсов. Импульсный характер, как правило, носят индустриальные помехи, создаваемые различными электрическими устройствами, а также атмосферой. На железнодорожном транспорте импульсные помехи создаются прежде всего контактной сетью электротяги и другими искрящими устройствами. В частности, следует отметить, что наиболее распространенными являются импульсные помехи, возникновение которых связано с напряжением промышленной частоты, причем момент возникновения импульсной помехи, совпадает с максимумами напряжения на токопроводящих проводах.
Часто импульсную помеху на выходе высокочастотной части (полосового фильтра) приемного устройства рассматривают как результат ударного возбуждения резонансных контуров (полосового фильтра) короткими одиночными импульсами, длительность которых меньше, а интервал следования больше времени существования переходных процессов в контурах.
При чисто импульсивном (неперекрывающемся) воздействии импульсная помеха на выходе узкополосного тракта на интервале [О, Т] может быть представлена в виде
где k— число импульсов в интервале [О, Т\;
(/иш; — случайная амплитуда импульсной помехи;
Основными статистическими характеристиками импульсных помех являются распределение вероятностей амплитуд импульсов, их длительности и временных интервалов между ними.
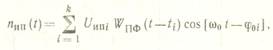
Для описания амплитуд и мгновенных значений импульсных помех в различных каналах передачи используются различные законы.
Считается, что широкий класс импульсных помех на железнодорожном транспорте описывается логарифмически нормальным законом распределения амплитуд и обобщенно — гауссовским распределением мгновенных значений при ударном возбуждении входных контуров.
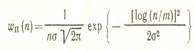
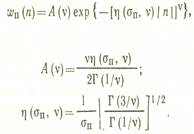
5-6.Разложение периодических сигналов в ряды Фурье по системе тригонометрических функций.
Если взять в качестве элементных
функций тригонометрические функции
T-интервал
ортогональности функции совпадающей с периодом колебаний то
ряд Фурье принимает следующий вид
это разложение
Фурье, Ао/2-является постоянной составляющей определяемой выражением в виде а
коэффициенты Ак и Вк называются коэффициентами разложения
Используя обобщенный коэффициент разложения в виде амплитуды составляющей гармоники Ак и начальную фазу составляющей jк можно записать ряд Фурье в следующем виде
В практических исследованиях часто пользуются комплексной формой записи ряда Фурье на основе известных формул Эйлера
Тогда 
Ак- комплексная амплитуда к-ой гармоники Она содержит данные и об амплитуде и о фазе к-ой гармоники . Спектр сигналов состоит из бесконечного множества составляющих, имеющих дискретный ряд частот задаваясь частотой кратной основной частоте, можно получить дискретный спектр. Спектр сигнала зависит от периода следований, чем больше период сигнала тем более сложным будет спектр этого сигнала т.е. число гармонических составляющих в спектральном составе колебаний.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.