
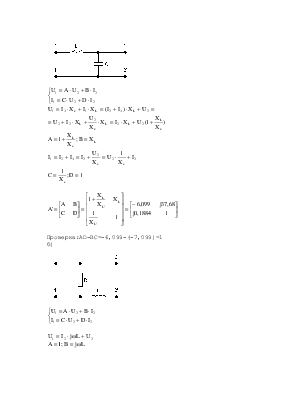




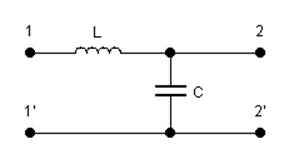
1.Исходная схема:
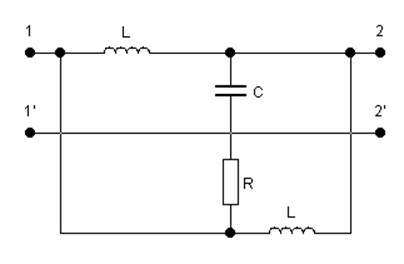
Преобразуем исходную схему:
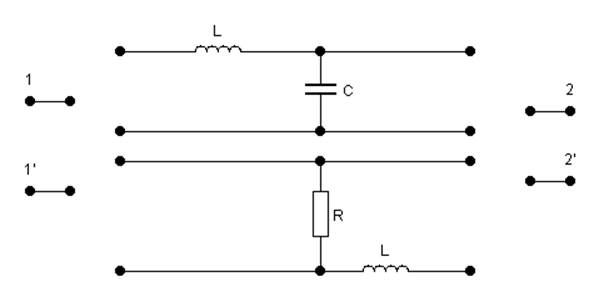
Представим сложный четырехполюсник в виде двух простых:
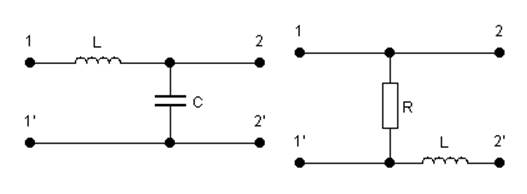
Способ соединения простых четырехполюсников- параллельный.
2.Определим коэффициенты матриц А простых четырехполюсников.
а)
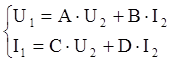
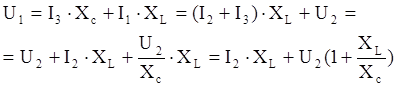
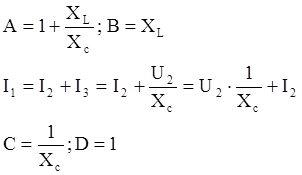
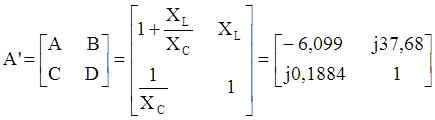
Проверка:AD-BC=-6,099-(-7,099)=1
б)
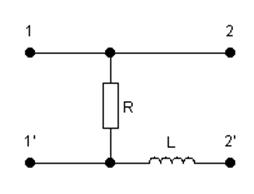
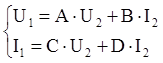
![]()
![]()
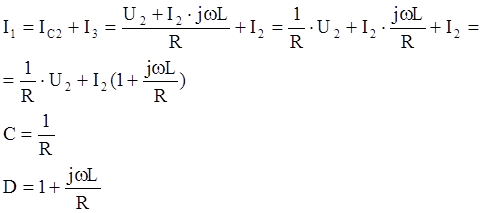
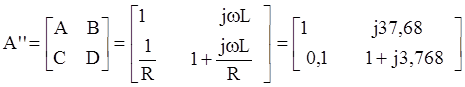
Проверка:AD-BC=1+j3,768-j3,768=1
3.Определим коэффициенты матрицы А составного четырехполюсника.
Так как соединение параллельное, то перейдем от матриц А' и A'' к матрицам Y' и Y''.
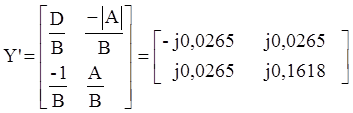
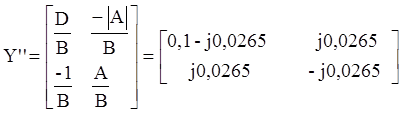
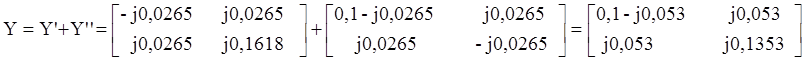
Перейдем от матрицы Y к матрице А составного четырехполюсника:
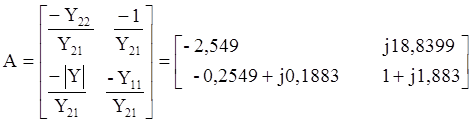
Проверка:AD-BC=-2,5409-j4,80606+3,549+j4,802=1
4.Определим собственные и рабочие параметры четырехполюсника.
Найдем характеристическое сопротивление и постоянную передачи четырехполюсника:
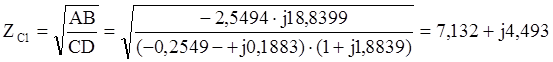
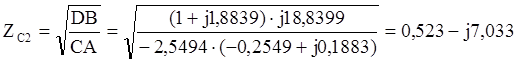
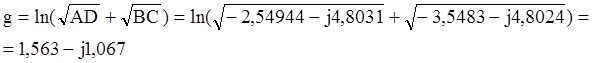
Так как g=a+jb, то а=1,563; b=-1,067
Определим входные сопротивления Zвх1 и Zвх2 относительно входных и выходных зажимов соответственно:
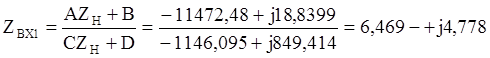
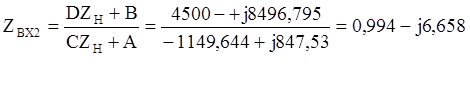
Определим рабочее затухание четырехполюсника
араб=а+а1+а2+а3

араб=1,563+1,7+2,539-0,044=5,758
Определим вносимое затухание четырехполюсника:
авн=араб-а4
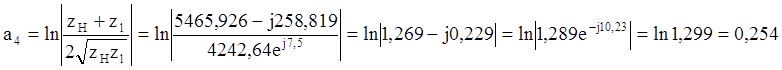
авн=5,758-0,254=5,504
5.Рассчитаем и построим зависимости модуля и аргумента входного сопротивления составного четырехполюсника от сопротивления нагрузки
Zвх1(Rн )и jвх1(Rн ).
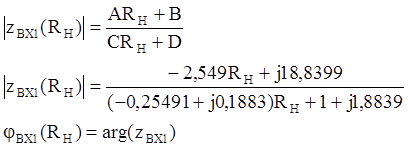
Результаты рассчетов сведем в таблицу:
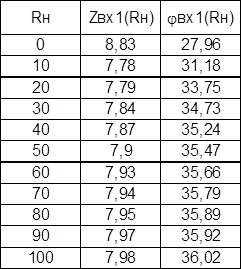
Графики представлены на рисунках 1 и 2.
6.Запишем уравнение передачи четырехполюсника в параметрической форме.
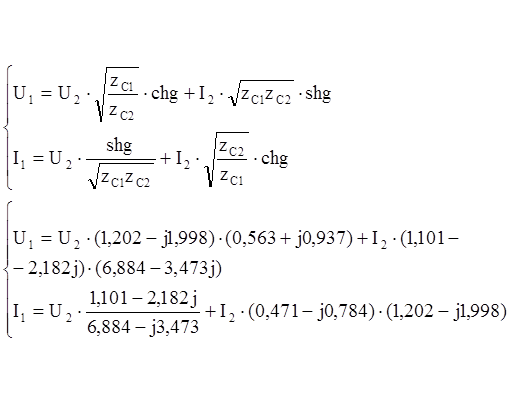
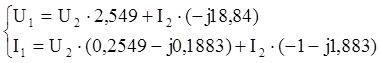
Запишем уравнение передачи четырехполюсника в матричной форме:
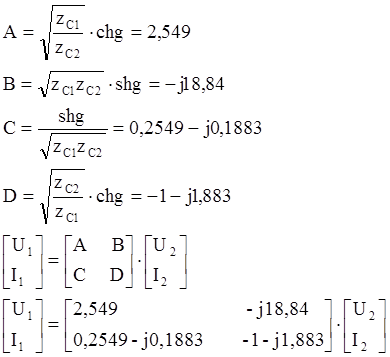
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.