Задача, №1
Для заданной схемы (рис. 1) требуется:
1.Классическим
методом определить закон изменения во времени токов всех ветвей схемы и
напряжений на катушке ![]() и конденсаторе
и конденсаторе ![]() .
.
2.Построить графики
изменения во времени тока в катушке ![]() и напряжения на её зажимах
и напряжения на её зажимах ![]() .
.
3.Операторным методом найти закон изменения во времени тока переходного процесса в катушке iL(t) или напряжения на конденсаторе uC(t).
Задача №2
На вход несимметричного
четырехполюсника (рис. 2) подается импульс напряжения ![]() длительностью
длительностью
![]() (график 3). Определить закон изменения во
времени напряжения
(график 3). Определить закон изменения во
времени напряжения ![]() и построить в масштабе его
график. Задачу решить с помощью интеграла Дюамеля.
и построить в масштабе его
график. Задачу решить с помощью интеграла Дюамеля.
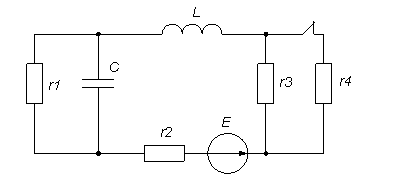
рис. 1

рис. 2
Решение.
Задача №1
Исходные расчётные данные:
E=30 B; r1=12 Ом;
L=95 мГн; r2=24 Ом;
С=120 мкФ; r3=17 Ом;
r4=9 Ом.
1.Классический метод
Схема электрической цепи:
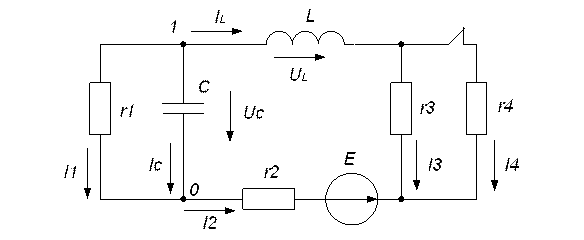
рис. 3
Составим уравнения для послекоммутационной схемы по законам Киргофа:
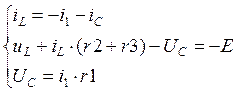
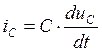
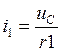
![]()
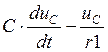
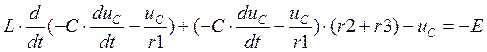
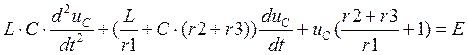 .
.
Решаем данное уравнение:
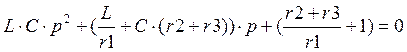
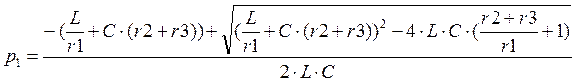
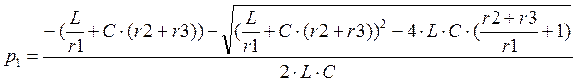
![]()
![]() .
.
Определим закон изменения напряжения на конденсаторе:
![]()
![]()
Находим независимые начальные условия:
Рассмотрим
докоммутационною схему, заменив в ней конденсатор разрывом цепи, а катушку –
коротко-замкнутой перемычкой. Определим при ![]()
![]() и
и ![]()
![]() , а
, а ![]()
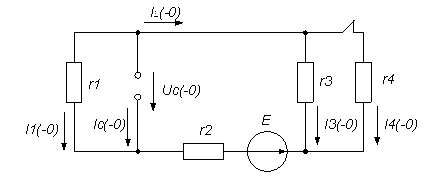
рис. 4
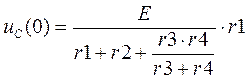
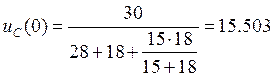 В
В
Так как ток ![]() , то ток
, то ток ![]() равен
равен ![]()
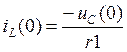
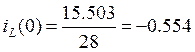 А
А
Находим зависимые начальные условия:
Рассмотрим послекоммутационную схему, в которой заменим катушку источником тока, а конденсатор – источником ЭДС:
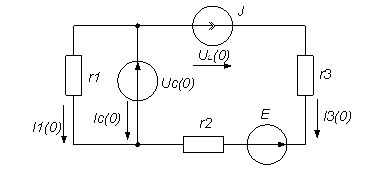
рис. 5
![]()
Решаем систему методом контурных токов:
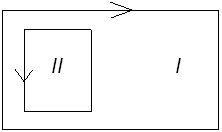
рис. 6
В первом контуре
контурный ток ![]() . Для нахождения второго
контурного тока достаточно только одного уравнения.
. Для нахождения второго
контурного тока достаточно только одного уравнения.
![]()
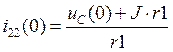
![]() В
В
![]()
![]() А
А
![]()
![]() А
А
Найдем напряжение на
катушке при ![]()
![]()
![]() В
В
Определим
принужденные составляющие тока ![]() и напряжения
и напряжения ![]() :
:
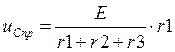 ,
, ![]() В ;
В ; 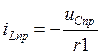 ;
; ![]() А.
А.
Найдем постоянные интегрирования:
![]()
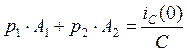
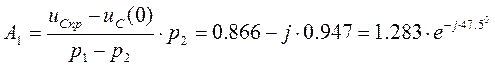
![]()
Для напряжения на конденсаторе:
![]()
![]() В
В
![]() В
В
Проверим для ![]()
![]() В
В
Определим ток ![]() :
:
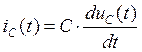
![]()
![]() А
А
Проверим для ![]()
![]() А
А
Найдем ток ![]()
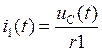
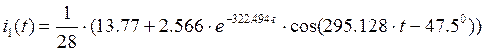 А
А
![]() А
А
Проверим для ![]()
![]() А
А
Из
схемы мы видим что ток ![]() можно определить как обратную
величину от суммы токов
можно определить как обратную
величину от суммы токов ![]() и
и ![]() :
:
![]()
![]() А
А
![]() А
А
Проверим для ![]()
![]() А
А
Определим напряжение
на катушке ![]() :
:
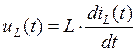
![]() В
В
![]() В
В
Проверим для ![]()
![]() В
В
2.Графики
изменения во времени напряжения ![]() и тока в катушке
и тока в катушке ![]() :
:
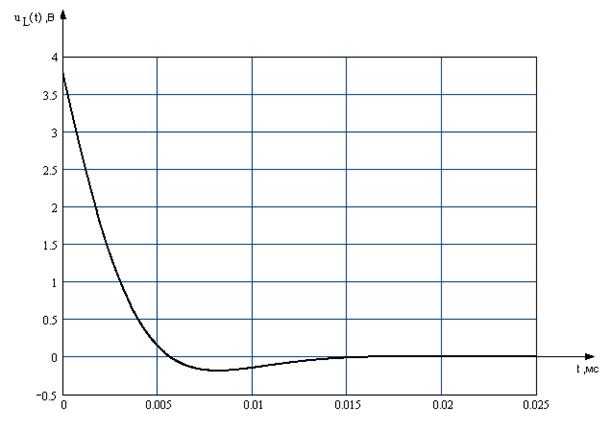
График 1
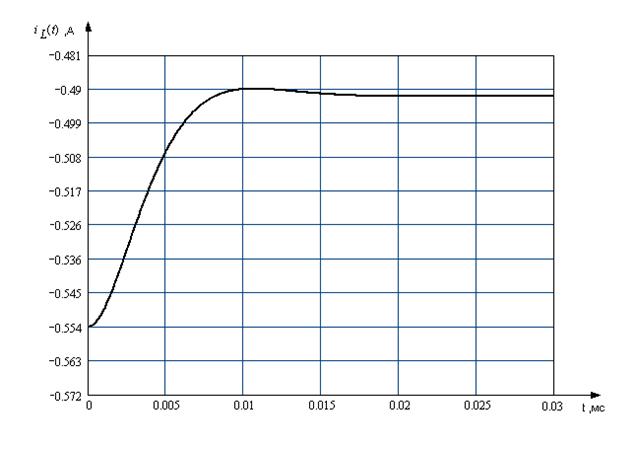
График 2
3.Операторный метод.
Операторная схема замещения:
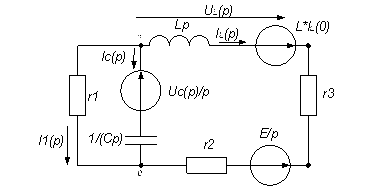
рис. 7
Независимые начальные условия вычисленные при расчете классическим методом:
![]() В
В
![]() А
А
Рассчитаем цепь методом узловых потенциалов, считая потенциал узла 0 равным нулю вольт.
![]() В
В
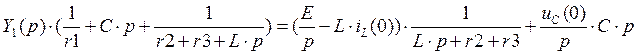
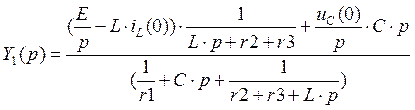
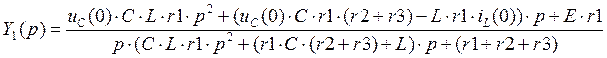 (1)
(1)
![]()
![]()
Определим значение ![]() при которых знаменатель выражения (1)
обращается в нуль:
при которых знаменатель выражения (1)
обращается в нуль:
![]()
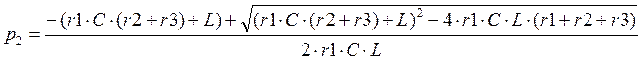
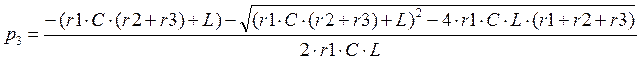
![]()
![]()
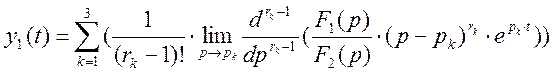
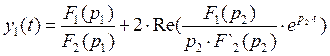 ;
;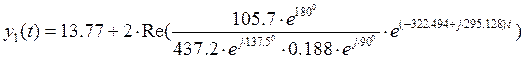 В
В
![]() В
В
Определим напряжение
![]() :
:
![]() ;
; ![]() В
В
Проверим для ![]()
![]() В
В
Задача №2
Исходные расчётные данные:
r1=10 Ом C=70 мкФ
r2=8 Ом ![]() =14
В
=14
В
r3=7 Ом ![]() c
c
|
,при |
|
,при |
|
,при |
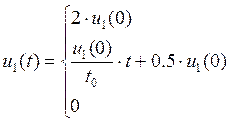
График 3
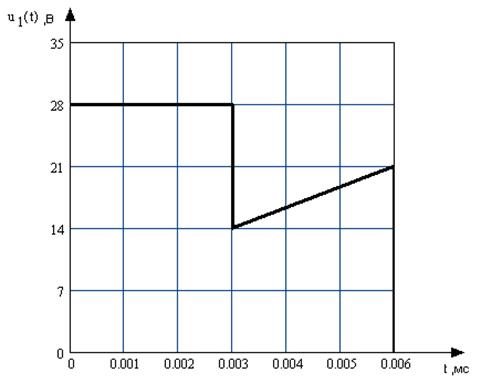
Найдем переходную функцию по напряжению для данной схемы

рис.8
Примем на входе цепи
напряжение ![]() равное одному вольту, тогда:
равное одному вольту, тогда:
![]()
или
![]()
Определим закон изменения напряжения на конденсаторе:
![]()
Начальные
независимые условия: ![]()
![]() В
В
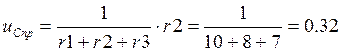 В
В
![]()
Составим операторную схему замещения:
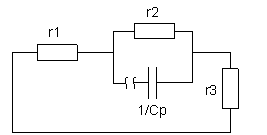
рис. 9
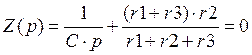
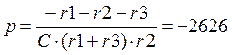
Определим постоянную
составляющую ![]()
![]()
![]()
![]()
Ток в цепи конденсатора
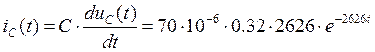
Определим ![]()
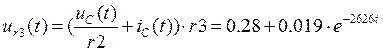
таким образом ![]()
![]()
Для интервала ![]() , где
, где 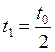
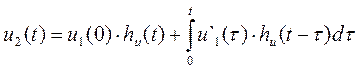
![]()
Для интервала ![]() , где
, где ![]()
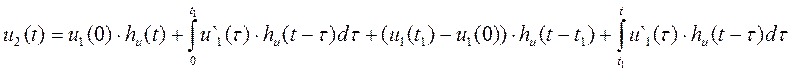
![]()
![]()
Для интервала ![]() :
:
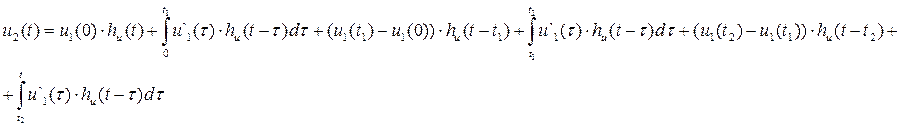
![]()
![]()
Таким образом функция напряжения будет принимать значения трёх различных функций на соответствующих интервалах.
|
,при
|
|
,при
|
|
,при
|
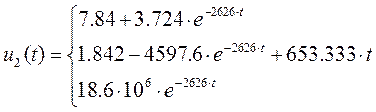
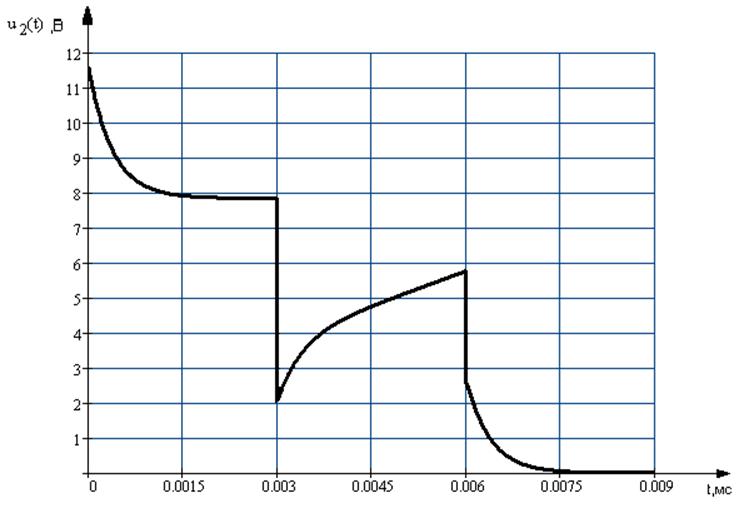
Построим график
функции ![]()
График 4
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.