Описание сигнала в виде кусочно-определенной функции, использую функцию piecewise пакета Maple

Пример выполнения пп. 1 - 11

(в пример внесена ошибка!, найти и исправить самостоятельно!)

1.        Описать заданный сигнал в виде кусочно-определенной функции (использовать функцию piecewise пакета Maple).

> restart;

> f:=x->piecewise(x>=0 and x<=t1,0,x>t1 and x<=t2,xm1*(x-t1)/(t2-t1),x>t2 and x<=t3,xm1*(t3-x)/(t3-t2),x>t3 and x<=t4,0,x>t4 and x<=t5,xm2*(x-t4)/(t5-t4),x>t5 and x<=t6,xm2*(t6-x)/(t6-t5),x>t6,0):

> xm1:=5:xm2:=-4:t1:=T/6:t2:=T/3:t3:=T/2:t4:=2*T/3:t5:=5*T/6:t6:=T:

> T:=2*Pi:

2.        Построить график полученной функции, убедиться в правильности описания сигнала.

> plot(f(x),x=0..T);

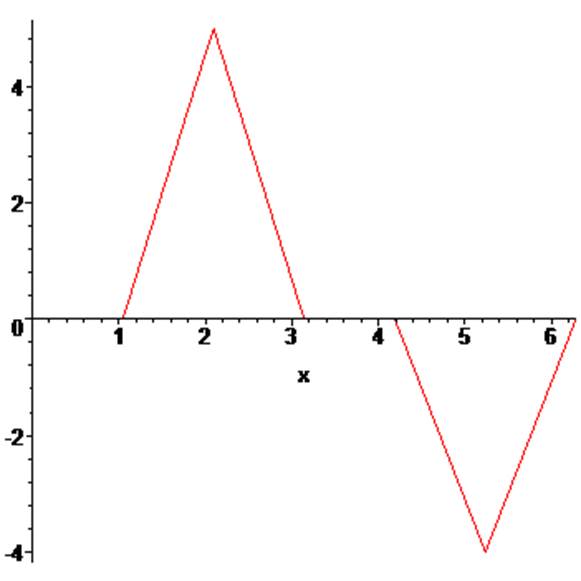
3-4.        Задавшись исходными данными для сигнала, получить аналитические зависимости для спектральной плотности сигнала, коэффициентов разложения в ряд Фурье, действительной и мнимой частей разложения, амплитудно-частотной и фазо-частотной характеристик.  

Построить графики полученных зависимостей.

Получим аналитические зависимости для спектральной плотности сигнала и построим график полученной зависимости:

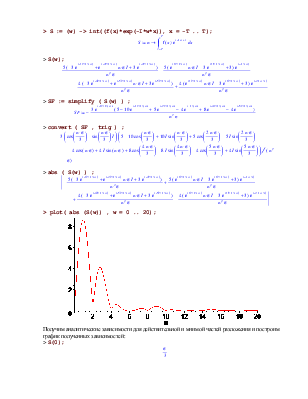
> S := (w) -> int((f(x)*exp(-I*w*x)), x = -T .. T);

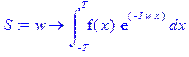
> S(w);

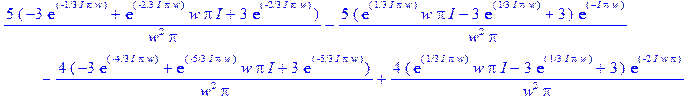
> SF := simplify ( S(w) ) ;

> convert ( SF , trig ) ;

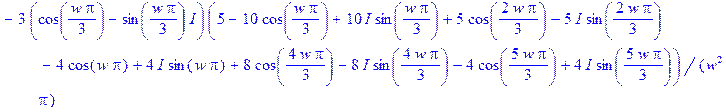
> abs ( S(w) ) ;

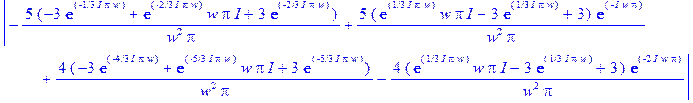
> plot( abs (S(w)) , w = 0 .. 20);

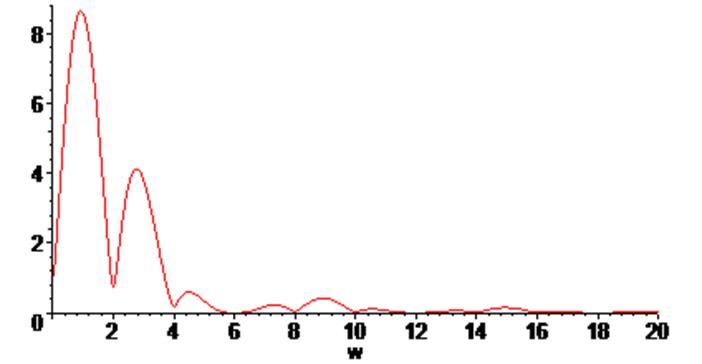
Получим аналитические зависимости для действительной и мнимой частей разложения и построим график полученных зависимостей:

> S(0);

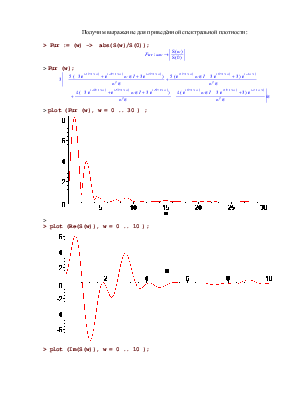
Получим выражение для приведённой спектральной плотности:

> Fur := (w) ->  abs(S(w)/S(0));

> Fur (w);

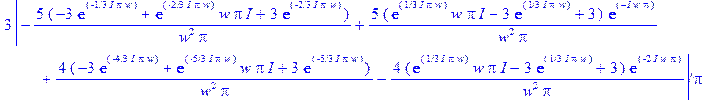
> plot (Fur (w), w = 0 .. 30 ) ;

>

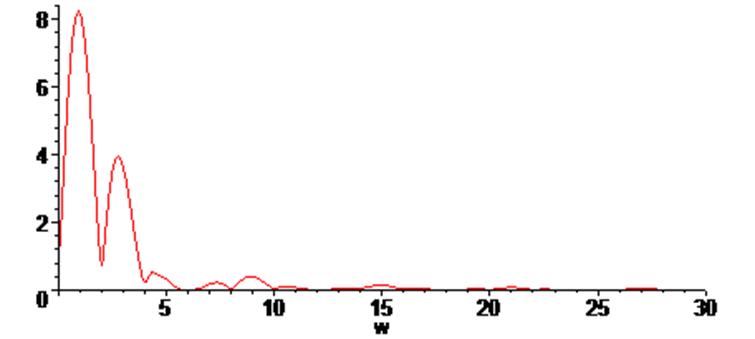
> plot (Re(S(w)), w = 0 .. 10 );

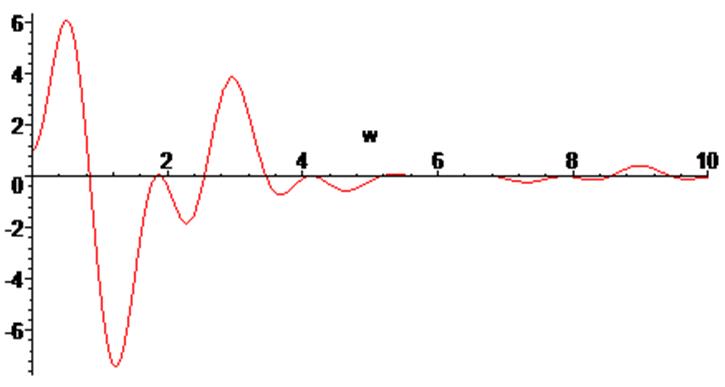
> plot (Im(S(w)), w = 0 .. 10 );

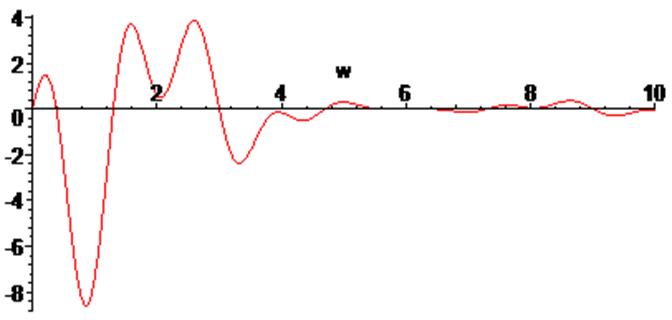
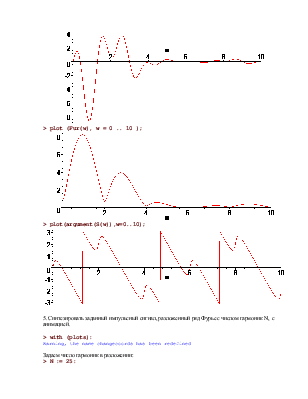
> plot (Fur(w), w = 0 .. 10 );

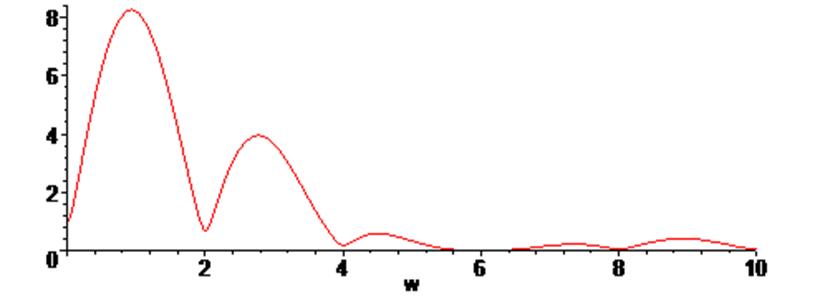
> plot(argument(S(w)),w=0..10);

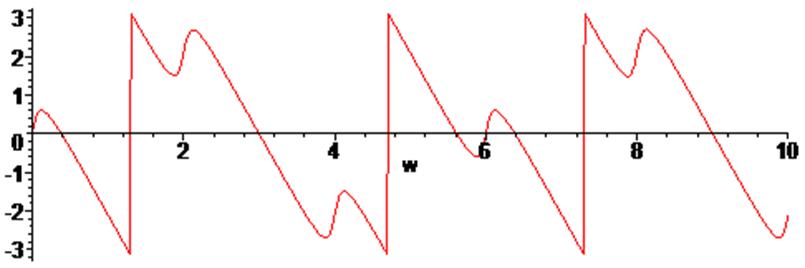
5. Синтезировать заданный импульсный сигнал, разложенный ряд Фурье с числом гармоник N,  с анимацией.

> with (plots):

Warning, the name changecoords has been redefined

Задаем число гармоник в разложении:

> N := 25:

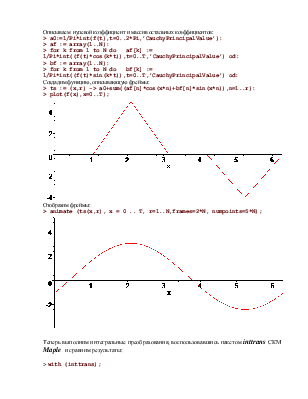
Описываем  нулевой коэффициент и массив остальных коэффициентов:

> a0:=1/Pi*int(f(t),t=0..2*Pi,'CauchyPrincipalValue'):

> af := array(1..N):

> for k from 1 to N do   af[k] := 1/Pi*int((f(t)*cos(k*t)),t=0..T,'CauchyPrincipalValue') od:

> bf := array(1..N):

> for k from 1 to N do   bf[k] := 1/Pi*int((f(t)*sin(k*t)),t=0..T,'CauchyPrincipalValue') od:

Создадим функцию, описывающую фреймы:

> ts := (x,r) -> a0+sum((af[n]*cos(x*n)+bf[n]*sin(x*n)),n=1..r):

> plot(f(x),x=0..T);

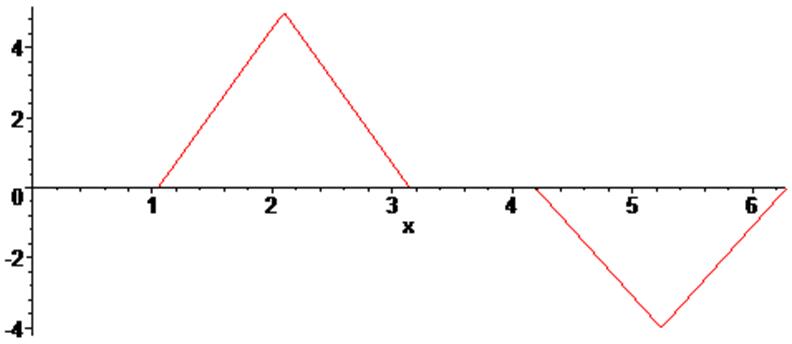
Отобразим фреймы:

> animate (ts(x,r), x = 0 .. T, r=1..N,frames=2*N, numpoints=5*N);

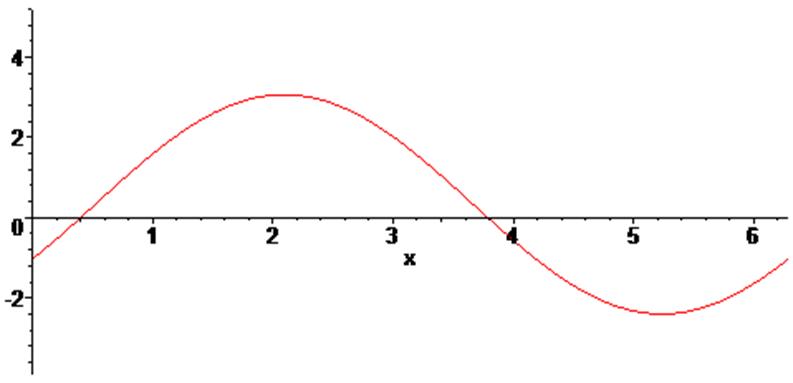
Теперь выполним интегральные преобразования, воспользовавшись пакетом inttransСКМMaple и сравним результаты:

> with (inttrans);

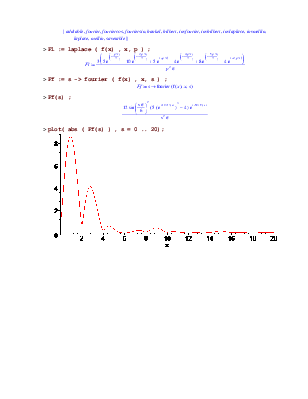
> Fl := laplace ( f(x) , x, p ) ;

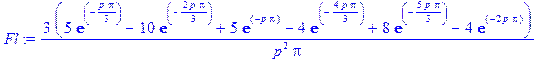
> Ff := s -> fourier ( f(x) , x, s ) ;

> Ff(s) ;

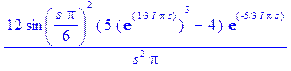
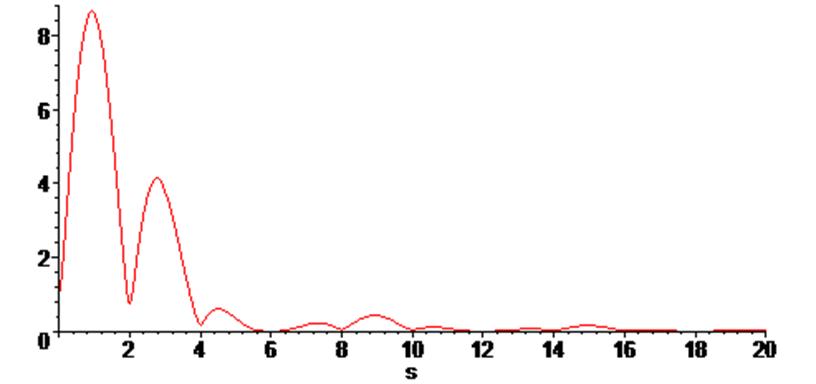
> plot( abs ( Ff(s) ) , s = 0 .. 20);