Моделирование и оптимизация теплотехнической системы автоматического регулирования температуры в помещении

МОДЕЛИРОВАНИЕ И ОПТИМИЗАЦИЯ ТЕПЛОТЕХНИЧЕСКОЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ТЕМПЕРАТУРЫ В ПОМЕЩЕНИИ

В настоящем примере разработана и описана система автоматического регулирования температуры в помещении, получены графики переходных процессов в системе компьютерной математики (СКМ) Maple, выполнено моделирование в пакете Simulink СКМ MatLab, проведена параметрическая оптимизация полученных переходных процессов.

            В настоящее время всё более актуальной становится задача проектирования и использования теплотехнических систем (ТС) небольшой и средней мощности, которые позволяют создавать автономные системы отопления, оптимизированные по энергопотреблению и которые могут использовать различные виды топлива. При этом современные подобные системы зачастую способны адаптироваться и перестраиваться под различные виды топлива, а система автоматики способна поддерживать оптимальные режимы энергопотребления. В силу того, что потребность в таких системах возрастает, актуальной становится задача автоматизации процесса расчета основных параметров оборудования теплотехнических систем и дальнейшего выбора компонент оборудования из числа известных.

В настоящее время разработаны, известны и описаны в литературе алгоритмы оптимального расчета и выбора параметров теплотехнических систем. Тем не менее, на рынке стран СНГ практически отсутствует доступные и надежные компьютерные программы подобных автоматических расчетов с последующим автоматизированным выбором элементов системы и их математическим описанием, на основе которого проектировщик мог бы выполнить моделирование и оптимизацию параметров проектируемой системы.

Необходимость в подобном моделировании продемонстрируем на следующем примере системы автоматического регулирования температуры в помещении (рисунок 1):

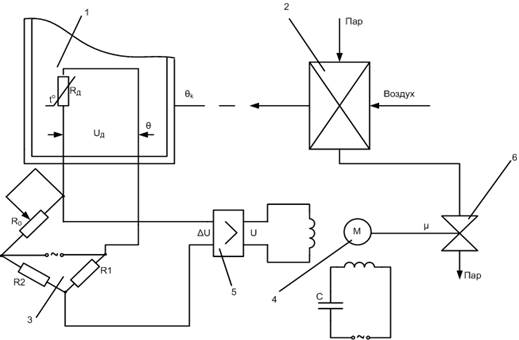
Рисунок 1 – Схема системы автоматического регулирования температуры в помещении: (1 – помещение; 2 – теплообменник (калорифер); 3 – измерительная мостовая схема; 4 – двухфазный исполнительный двигатель; 5 – дифференциальный магнитный усилитель; 6 – клапан (заслонка))

Математическую модель объекта регулирования (помещения) определяют на основе уравнения теплового баланса 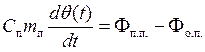[1]:

,                                                                                                        (1)

где С_п – усредненная теплоемкость, определяемая теплоемкостями воздуха и предметов, находящихся в помещении; m_п – усредненная масса, определяемая массами воздуха и предметов, находящихся в помещении;  – температура воздуха в помещении, Ф_п.п. – поток теплоты, поступающий в помещение от калорифера; Ф_о.п.– поток теплоты, отводимый из помещения через стенки в окружающую среду.

В свою очередь,

                                                                                                    (2)

где α_к – коэффициент теплоотдачи калорифера, F_к – площадь поверхности нагревательного элемента (калорифера),  – температура воздуха на выходе калорифера.

                                                                                                     (3)

где α_о – коэффициент теплоотдачи стен помещения, F_о – площадь теплоотдающей поверхности стен помещения, f(t) – возмущающее воздействие на объекте регулирования.

С учетом выражений (2) и (3) уравнение (1) примет вид:

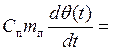
-.                                                       (4)

После раскрытия скобок и дальнейших несложных преобразований оно запишется в виде:

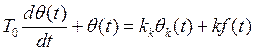,                                                                                              (5)

где T₀ – постоянная времени, с, при этом

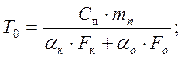
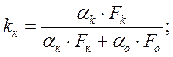
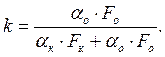
Математическую модель регулирующего органа (калорифера) определяют аналогичным образом на основании теплового баланса:

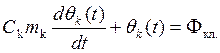 - Ф_п.п. ,

где С_k – усредненная теплоемкость для калорифера; m_k – усредненная масса для калорифера; Ф_кл. – поток теплоты, поступающий в калорифер при открытии клапана.

Данное уравнение можно записать следующим образом:

,

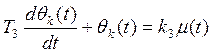где T₃– постоянная времени, с;  θ_k(t)– значение температуры воздуха на выходе калорифера, ºС;  k₃ – коэффициент передачи;  μ(t) – линейное перемещение клапана, см.

Математическую модель воспринимающего органа (датчика) можно записать следующим образом

,

где θ(t) – значение температуры воздуха в помещении, ºС; k₁ – коэффициент передачи; U_Д(t) – падение напряжения на термодатчике, В.

Таким образом, полная модель подобной теплотехнической системы и динамические свойства объекта регулирования и элементов системы описываются следующими уравнениями:

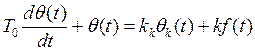 - объект регулирования;

 - датчик;

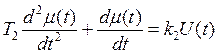 - двигатель совместно с клапаном;

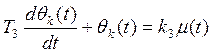 - калорифер;

 - сравнивающий орган;

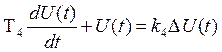 - магнитный усилитель,

где T₀, T₂, T₃, T₄ – постоянные времени, с; θ(t) – значение температуры воздуха в помещении,ºС; θ_k(t) – значение температуры воздуха на выходе калорифера,ºС; , k, k₁, k₂, k₃, k₄ – коэффициенты передачи; f(t) – возмущающее воздействие на объекте регулирования; U_Д(t) – падение напряжения на термодатчике, В;  – напряжение на выходе мостовой схемы (сигнал рассогласования), В; μ(t) – линейное перемещение клапана, см; U₀  – задающий сигнал, В.