Решение системы
уравнений в СКМ Maple приведён
в файле ModelTeploTechn.mws.
При параметрах системы T0=1000 c; T2=0.06 c; T3=20 c; T4=0.5 c; 
=1; k=0.2;
k1=0.2 В/ºC; k2=0.002 см/(В·с); k3=10
ºC/см; k4=2; f=-11 ºC; U0=4
В, был получен следующий график (рисунок 2) переходного процесса нагрева
температуры в комнате от 5 до 20 градусов при температуре наружного воздуха -11
ºС.
Листинг программы на языке Maple приведён ниже.
В переменную Du занесена система уравнений, в переменную Ds – функции, относительно которых решается система. Начальные
условия написаны в переменную Nu. При этом z(t) – функция изменения
температуры в помещении 
(t), zk(t) – функция изменения значения температуры воздуха на
выходе калорифера θk(t), m(t)
– функция линейного перемещения клапана μ(t),
U0 – задающий сигнал, f(t) – функция возмущающего воздействия на объекте
регулирования.
> restart;
> Du := T0*diff (z(t), t) + z(t) = Kk*zk(t) + k*f(t) , T2*diff(m(t), t$2) + diff(m(t), t) = k2*U(t) , T3*diff(zk(t), t) + zk(t) = k3*m(t) , T4*diff(U(t), t) + U(t) = k4*(U0 - k1*z(t) );
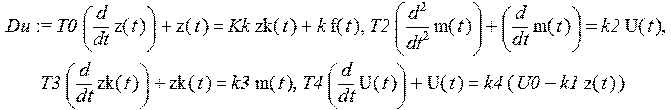
> Ds := { zk(t) , m(t), U(t), z(t) } :
> Nu := zk(0) = 0 , m(0) = 2, D(m)(0) = 0 , U(0) = 0.2, z(0) = 5 :
Температурный датчик и резистор задания входного воздействия проградуированы таким образом, что, например, температуре 20ºС соответствует напряжение 4В. Далее зададим параметры системы уравнений и решим её численно; затем при помощи функции odeplot построим график изменения температуры в помещении на интервале от 0 до 30000 с.
> T0:=1000: T2:=0.06: Kk :=1: k:=0.2: k1:=0.2: k4:=2: k2:=0.002: k3:=10: T3:=20: T4:=0.5: f:=-11: U0:=4:
> Du;
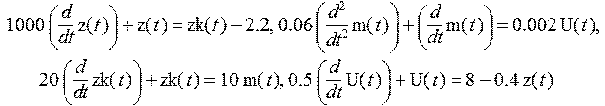
> Rs := dsolve ( {Du , Nu} , Ds , type = numeric , maxfun=5000000 ) ;
> with (plots):
> odeplot ( Rs , [ t, z(t) ] , t = 0 .. 30000 , numpoints = 500) ;
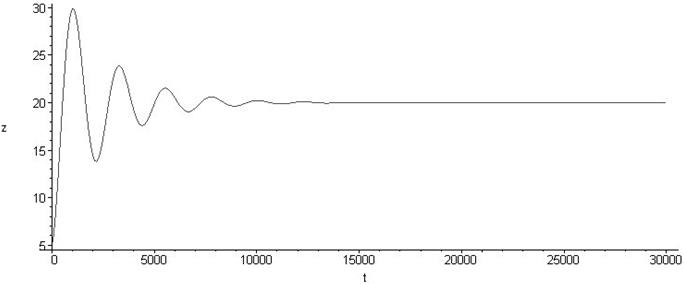
Рисунок 2 - График нагрева температуры в комнате
Для этой же системы была получена модель в виде передаточных функций и выполнено моделирование в пакете Simulink СКМ MatLab (рисунок 3). Модель находится в файле ModelTeploTechn.mdl .
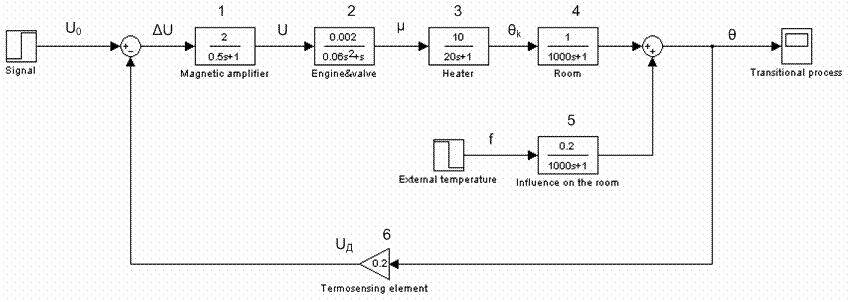
Рисунок 3 - Модель ТС в пакете Simulink
И наконец приведённую выше систему уравнений можно свести к системе, разрешённой относительно первых производных (форма Коши), что позволяет выполнить её решение в блоке DEE СКМ MatLab. Пример приведён в файле ModelTeploTechnDEE.mdl .Рекомендуется самостоятельно его разобрать и выполнить моделирование, изменяя параметры входных воздействий и модели.
Результаты, как и следовало ожидать, оказались аналогичными с моделированием в СКМ Maple. Математическое моделирование показывает, что система автоматического управления ТС с серийными параметрами приводит её в требуемое состояние, т.е. в помещении устанавливается температура 20ºС. Но при этом очевиден колебательный режим процесса, который не так просто отследить в эксплуатационном режиме. Таким образом, наличие системы автоматики не только не гарантирует оптимизации энергопотребления, но может даже приводить к неоправданным потерям. Очевидно, что при проектировании ТС необходимо рассчитывать и по возможности оптимизировать параметры её элементов.
На рисунке 4 показан процесс нагрева при оптимизированных параметрах системы. Критериями оптимизации процесса изменения температуры на объекте регулирования (в помещении) являются время переходного процесса и величина перерегулирования. Оптимизируемый параметр - коэффициент передачи двигателя совместно с клапаном (блок 2 на структурной схеме). Исходное значение коэффициента 0.002. После выполнения оптимизационного поиска он принял следующее значение: 0.00015625.
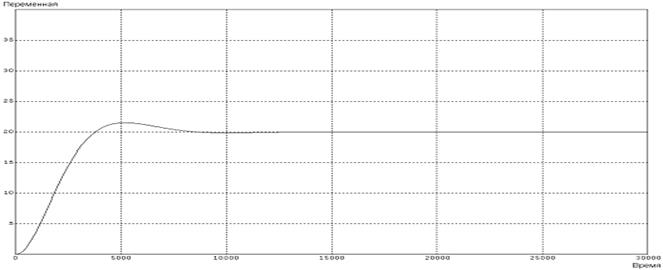
Рисунок 4 - Процесс нагрева при оптимизированных параметрах системы
Как видно из вышеприведенных рисунков, до оптимизации во время переходного процесса температура в помещении может достигать максимума в 30ºC и минимума в 14ºC. После оптимизации максимум температуры снижается до 22ºC, минимум повышается и лишь на сотые доли не достигает установившихся 20ºC. Значительно уменьшилось и время переходного процесса: с 9000с до оптимизации до 2600с после процесса оптимизации. Расчет показывает, что при подобном режиме потери теплоносителя для нагрева помещения уменьшаются не менее чем на 10% по сравнению с неоптимизированной системой рассматриваемого примера.
Еще более актуальной решение подобной проблемы оптимизации возникает при распределенных ТС. Моделирование показывает, что неоптимизированные системы автоматики не только не экономят энергоносители, но приводят к неоправданным их потерям. Выполняемая работа должна завершиться созданием доступного для проектных организация и служб эксплуатации инструмента моделирования и оптимизации параметров как автономных, так и распределённых ТС.
СПИСОК ЛИТЕРАТУРЫ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.