



Математическое моделирование технических систем с нелинейными характеристиками
Для выполнения работы параметры аппроксимирующих функций необходимо взять из лабораторной работы по изучению методов регрессионного анализа, выполненной ранее.
В настоящем примере аппроксимирующие кривые будут заново получены в ходе его выполнения.
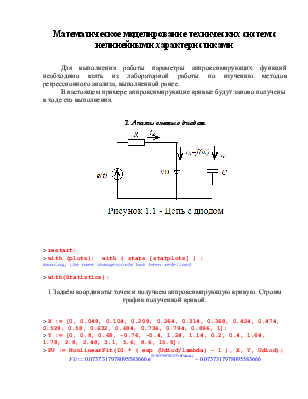
1. Анализ схемы с диодом
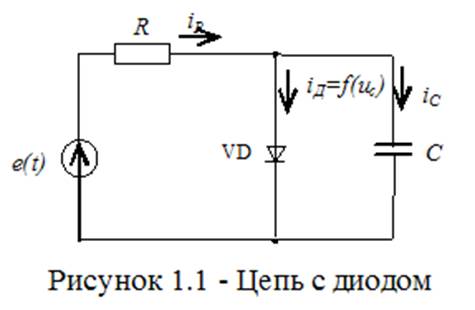
> restart:
> with (plots): with ( stats [statplots] ) :
Warning, the name changecoords has been redefined
> with(Statistics):
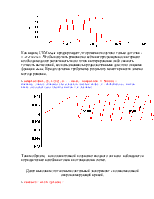
1 Задаём координаты точек и получаем аппроксимирующую кривую. Строим график полученной кривой.
> X := [0, 0.048, 0.104, 0.208, 0.264, 0.314, 0.368, 0.424, 0.474, 0.528, 0.58, 0.632, 0.684, 0.736, 0.794, 0.896, 1]:
> Y := [0, 0.8, 0.68, -0.76, -0.4, 1.24, 1.14, 0.2, 0.4, 1.64, 1.78, 2.8, 2.48, 3.1, 5.6, 8.6, 15.8]:
> FU := NonlinearFit(I0 * ( exp (Udiod/lambda) - 1 ), X, Y, Udiod);
![]()
> G := plot (FU, Udiod = 0 .. 1 ) :
> plots [display] ( {scatterplot(X,Y), G } ) ;
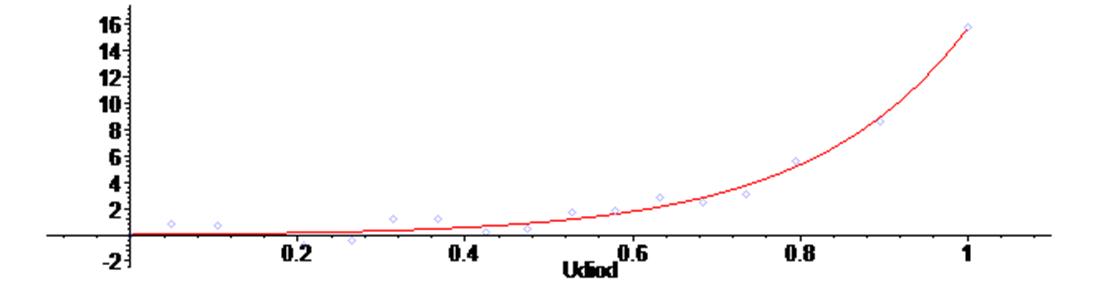
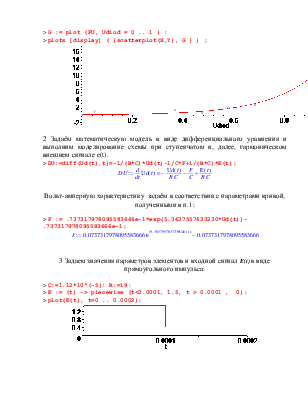
2 Задаём математическую модель в виде дифференциального уравнения и выполним моделирование схемы при ступенчатом и, далее, гармоническом внешнем сигнале e(t).
> DU:=diff(Ud(t),t)=-1/(R*C)*Ud(t)-1/C*F+1/(R*C)*E(t);
![]()
Вольт-амперную характеристику задаём в соответствии с параметрами кривой, полученными в п.1:
> F := .737317978095583666e-1*exp(5.3637557633230*Ud(t))-.737317978095583666e-1;
![]()
3 Задаем значения параметров элементов и входной сигнал E(t) в виде прямоугольного импульса:
> C:=1.12*10^(-5): R:=19:
> E := (t) -> piecewise (t<0.0001, 1.5, t > 0.0001 , 0):
> plot(E(t), t=0 .. 0.0002);

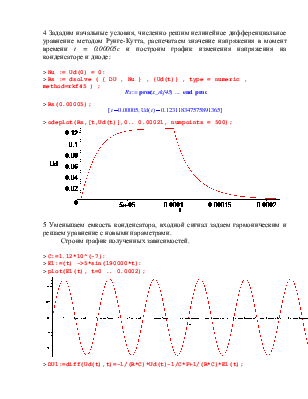
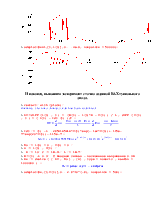
4 Зададим начальные условия, численно решим нелинейное дифференциальное уравнение методом Рунге-Кутта, распечатаем значение напряжения в момент времени t = 0.00005c и построим график изменения напряжения на конденсаторе и диоде:
> Nu := Ud(0) = 0:
> Rs := dsolve ( { DU , Nu } , {Ud(t)} , type = numeric , method=rkf45 ) ;
![]()
> Rs(0.00005);
![]()
> odeplot(Rs,[t,Ud(t)],0.. 0.00021, numpoints = 500);
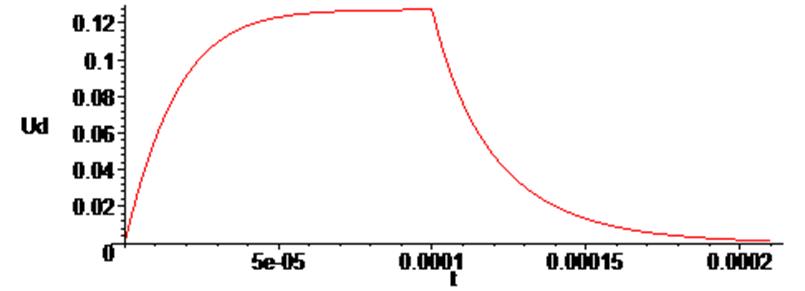
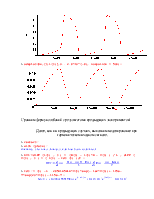
5 Уменьшаем емкость конденсатора, входной сигнал задаем гармоническим и решаем уравнение с новыми параметрами.
Строим график полученных зависимостей.
> C:=1.12*10^(-7):
> E1:=(t) ->5*sin(190000*t):
> plot(E1(t), t=0 .. 0.0002);
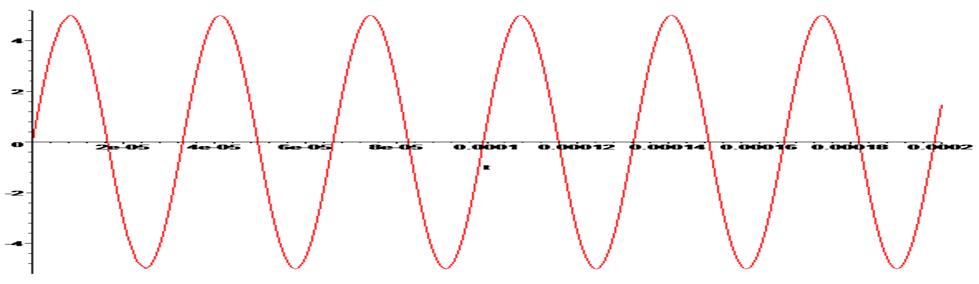
> DU1:=diff(Ud(t),t)=-1/(R*C)*Ud(t)-1/C*F+1/(R*C)*E1(t);
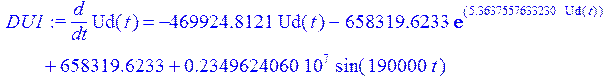
> Rs1 := dsolve ( { DU1 , Nu } , {Ud(t)} , type = numeric , method=rkf45 ) ;
![]()
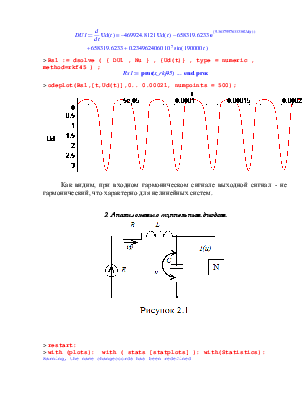
> odeplot(Rs1,[t,Ud(t)],0.. 0.00021, numpoints = 500);
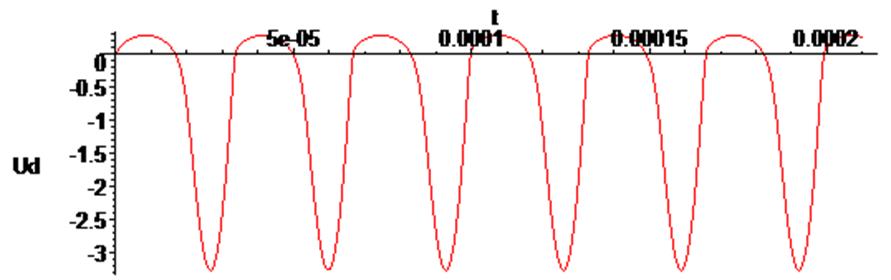
Как видим, при входном гармоническом сигнале выходной сигнал - не гармонический, что характерно для нелинейных систем.
2. Анализ схемы с туннельным диодом
> restart:
> with (plots): with ( stats [statplots] ): with(Statistics):
Warning, the name changecoords has been redefined
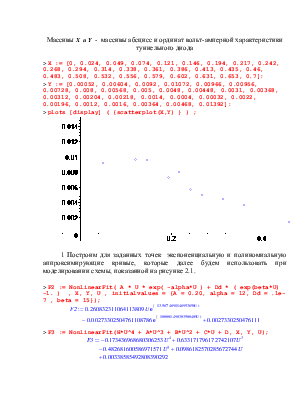
Массивы X и Y - массивы абсцисс и ординат вольт-амперной характеристики туннельного диода
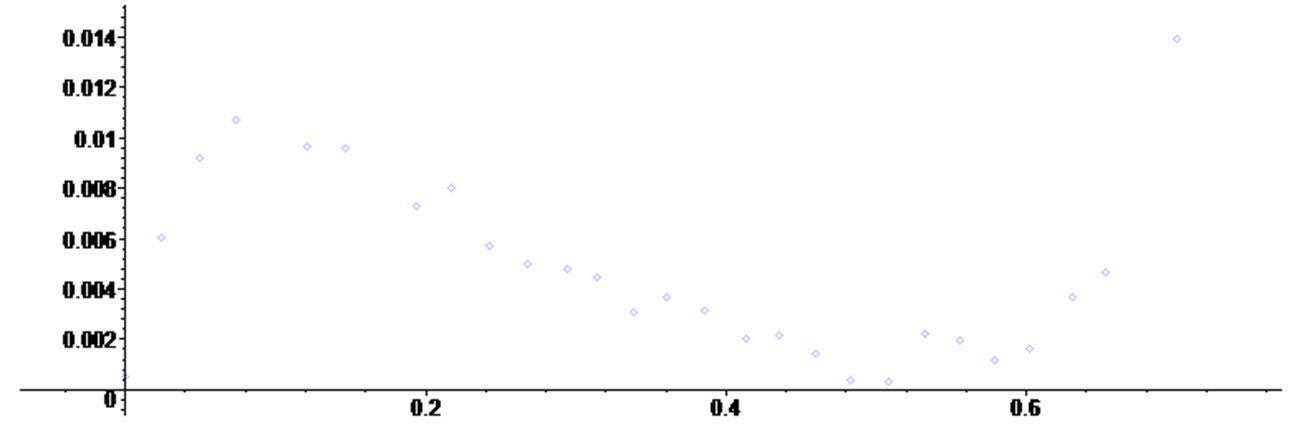
> X := [0, 0.024, 0.049, 0.074, 0.121, 0.146, 0.194, 0.217, 0.242, 0.268, 0.294, 0.314, 0.338, 0.361, 0.386, 0.413, 0.435, 0.46, 0.483, 0.508, 0.532, 0.556, 0.579, 0.602, 0.631, 0.653, 0.7]:
> Y := [0.00052, 0.00604, 0.0092, 0.01072, 0.00966, 0.00956, 0.00728, 0.008, 0.00568, 0.005, 0.0048, 0.00448, 0.0031, 0.00368, 0.00312, 0.00204, 0.00218, 0.0014, 0.0004, 0.00032, 0.0022, 0.00196, 0.0012, 0.0016, 0.00364, 0.00468, 0.01392]:
> plots [display] ( {scatterplot(X,Y) } ) ;
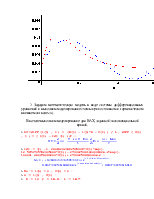
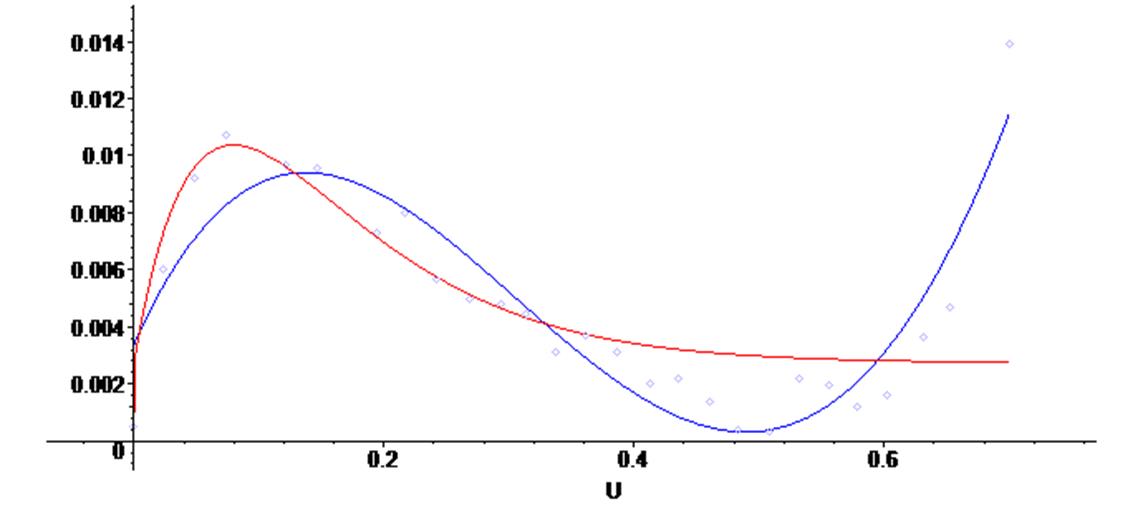
1 Построим для заданных точек экспоненциальную и полиномиальную аппроксимирующие кривые, которые далее будем использовать при моделировании схемы, показанной на рисунке 2.1.
> F2 := NonlinearFit( A * U * exp( -alpha*U ) + Dd * ( exp(beta*U) -1. ) , X, Y, U , initialvalues = {A = 0.20, alpha = 12, Dd = .1e-7 , beta = 15});
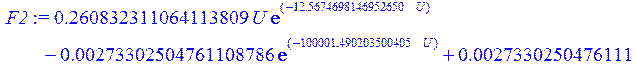
> F3 := NonlinearFit(H*U^4 + A*U^3 + B*U^2 + C*U + D, X, Y, U);
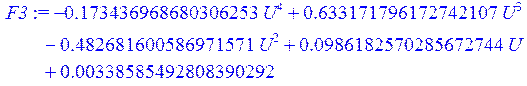
> G2 := plot (F2, U = 0 .. 0.7):
> G3 := plot (F3, U = 0 .. 0.7 , color = blue ) :
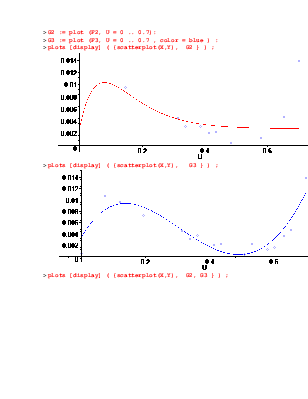
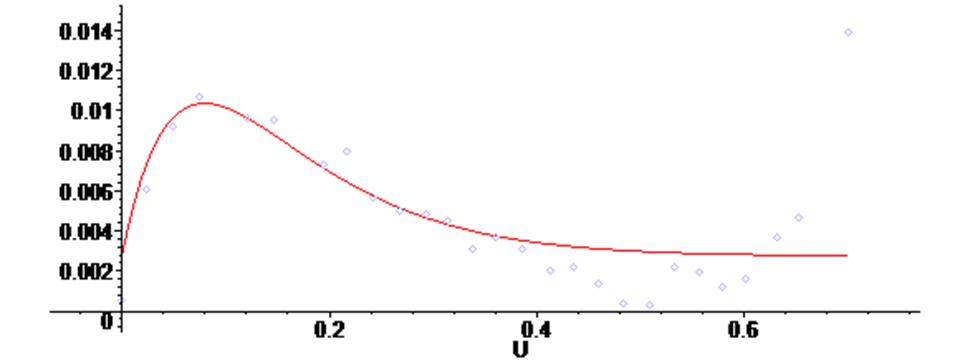
> plots [display] ( {scatterplot(X,Y), G2 } ) ;
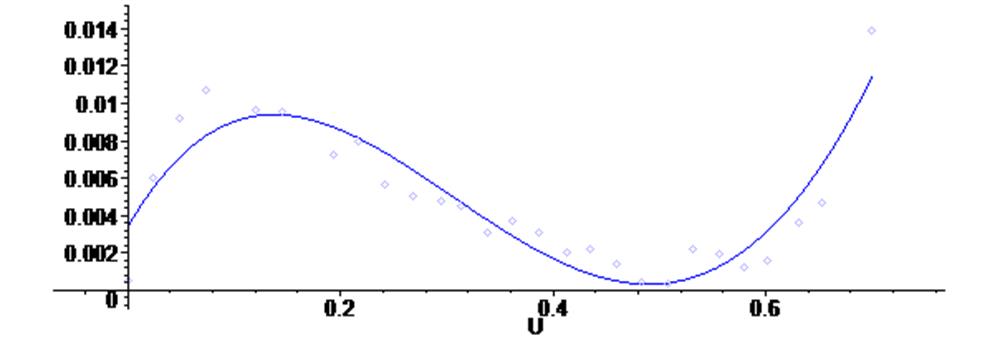
> plots [display] ( {scatterplot(X,Y), G3 } ) ;
> plots [display] ( {scatterplot(X,Y), G2, G3 } ) ;
2 Зададим математическую модель в виде системы дифференциальных уравнений и выполним моделирование схемы при постоянном и гармоническом внешнем сигнале e(t).
В начале выполним моделирование для ВАХ, заданной экспоненциальной кривой.
> DU:=diff (i(t) , t ) = (E(t) - i(t)*R - U(t) ) / L , diff ( U(t) , t ) = ( i(t) - Idt (t) )/C ;
![]()
> Idt := (t) -> .260832323382505338*U(t)*exp(-12.5674705762305906*U(t))-.273302536160403842e-2*exp(-100001.490076061804*U(t))+.27330253616040e-2 ;
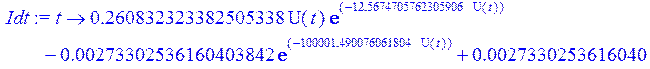
> Nu := i(0) = 0 , U(0) = 0 :
> S := i(t) , U(t) :
> R := 10: C := 1E-11: L := 1E-7:
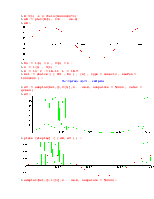
Входной сигнал E в первом вычислительном эксперименте - постоянное напряжение 0.3В
> E:=(t) -> 0.3:
Для решения задачи потребуется указать число точек интегрирования опцией maxfun = 1000000 , существенно увеличив по сравнению со значением "по умолчанию". Без применения опции maxfun в ряде случаев решение может быть не получено на всем требуемом промежутке. Следует иметь ввиду, что увеличение точек интегрирования, очевидно, увеличивает время решения систем уравнений.
> Rs := dsolve ( { DU , Nu } , {S} , type = numeric , maxfun = 1000000 ) ;
![]()
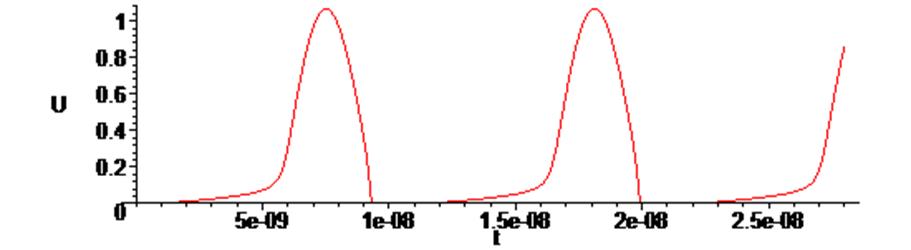
> odeplot(Rs,[t,U(t)],0.. 2.8*10^(-8), numpoints = 500);
> odeplot(Rs,[t,i(t)],0.. 2.8*10^(-8), numpoints = 500);
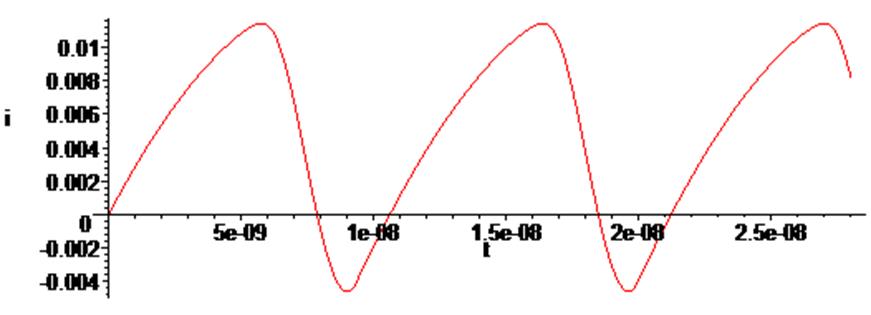
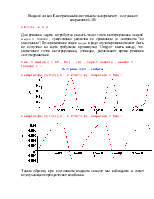
Таким образом, при постоянном входном сигнале мы наблюдаем в схеме незатухающие периодические колебания.
Далее выполним моделирование при гармоническом входном сигнале E(t) = 0.3*sin(19000000*t).
> restart:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.