Математическое моделирование технических систем с нелинейными характеристиками (Лабораторная работа № 9), страница 2

> with (plots):

Warning, the name changecoords has been redefined

> DU1:=diff (i(t) , t ) =  (E(t) - i(t)*R - U(t) ) / L , diff ( U(t) , t ) = ( i(t) - Idt (t) )/C ;

> Idt := (t) -> .260832323382505338*U(t)*exp(-12.5674705762305906*U(t))-.273302536160403842e-2*exp(-100001.490076061804*U(t))+.27330253616040e-2 ;

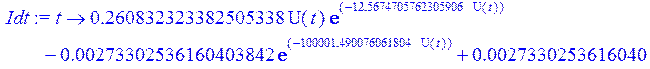
> E:=(t) -> 0.3*sin(19000000*t);

> plot(E(t), t=0 .. .4e-6);

> Nu := i(0) = 0 , U(0) = 0 :

> S := i(t) , U(t) :

> R := 10: C := 1E-11: L := 1E-7:

> Rs1 := dsolve ( { DU1 , Nu } , {S} , type = numeric , maxfun = 10000000 ) ;

> odeplot(Rs1,[t,U(t)],0.. .4e-6, numpoints = 50000);

Warning, cannot evaluate the solution further right of .21418028e-6, maxfun limit exceeded (see ?dsolve,maxfun for details)

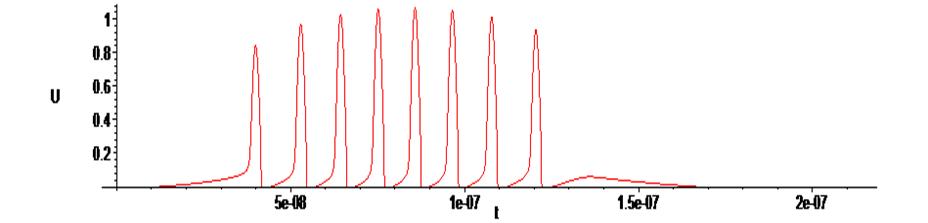
Как видим, СКМ Maple предупреждает, что решение получено только до точки t = .21418028e-6 . Чтобы получить решение на всём интересующем нас интервале необходимо далее увеличивать число точек интегрирования либо снижать точность вычислений, воспользовавшись предназначенными для этого опциями функции dsolve. В ряде случаев к требуемому результату может привести замена метода решения.

> odeplot(Rs1,[t,i(t)],0.. .4e-6, numpoints = 50000);

Warning, cannot evaluate the solution further right of .21418028e-6, maxfun limit exceeded (see ?dsolve,maxfun for details)

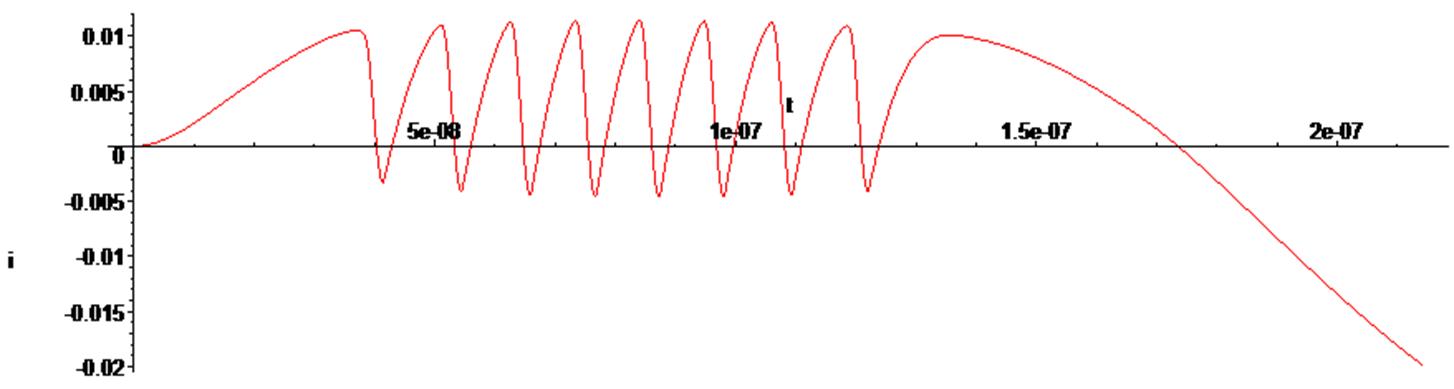
Таким образом,  на положительной полуволне входного сигнала  наблюдаются периодические колебания токов и потенциалов в схеме.

Далее выполним этот же вычислительный эксперимент c полиномиальной аппроксимирующей кривой.

> restart: with (plots):

Warning, the name changecoords has been redefined

> DUS:=diff (i(t) , t ) =  (E(t) - i(t)*R - U(t) ) / L , diff ( U(t) , t ) = ( i(t) - Idt (t) )/C ;

> Idt := (t) -> -.173436968680306253*U(t)^4+.633171796172742107*U(t)^3-.482681600586971571*U(t)^2+.986182570285672744e-1*U(t)+.338585492808390292e-2 ;

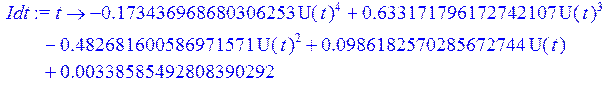
> Nu := i(0) = 0 , U(0) = 0 :

> S := i(t) , U(t) :

> R := 10: C := 1E-11: L := 1E-7:

> E:=(t) -> 0.3:  # Входной сигнал - постоянное напряжение 0.3В

> RsS := dsolve ( { DUS , Nu } , {S} , type = numeric , maxfun = 1000000 ) ;

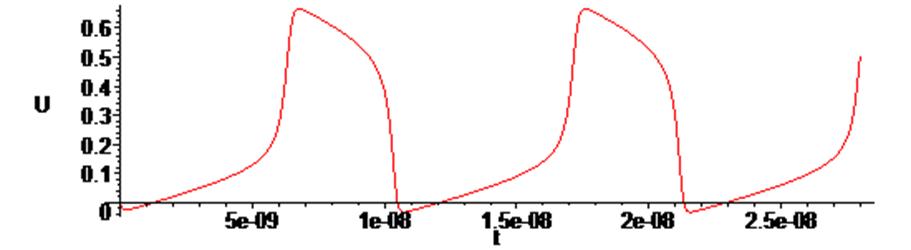
> odeplot(RsS,[t,U(t)],0.. 2.8*10^(-8), numpoints = 500);

> odeplot(RsS,[t,i(t)],0.. 2.8*10^(-8), numpoints = 500);

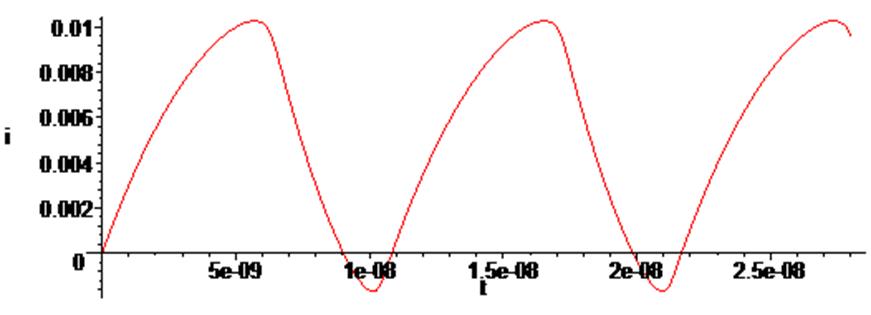
Таким образом, при постоянном входном сигнале мы опять наблюдаем в схеме незатухающие колебания, но  их характеристики отличаются  от предыдущего эксперимента.

Далее выполним моделирование при гармоническом входном сигнале и полиномиальной аппроксимирующей кривой.

> restart: with (plots):

Warning, the name changecoords has been redefined

> DUS1:=diff (i(t) , t ) =  (E(t) - i(t)*R - U(t) ) / L , diff ( U(t) , t ) = ( i(t) - Idt (t) )/C ;

> Idt := (t) -> -.173436968680306253*U(t)^4+.633171796172742107*U(t)^3-.482681600586971571*U(t)^2+.986182570285672744e-1*U(t)+.338585492808390292e-2 ;

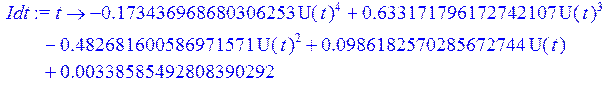
Задаём гармонический входной сигнал:

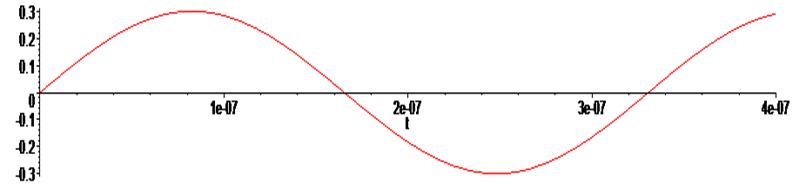
> E:=(t) -> 0.3*sin(19000000*t);

> plot(E(t), t=0 .. .4e-6);

> Nu := i(0) = 0 , U(0) = 0 :

> S := i(t) , U(t) :

> R := 10: C := 1E-11: L := 1E-7:

> RsS1 := dsolve ( { DUS1 , Nu } , {S} , type = numeric , maxfun=1000000 ) ;

> odeplot(RsS1,[t,U(t)],0.. .4e-6, numpoints = 50000);

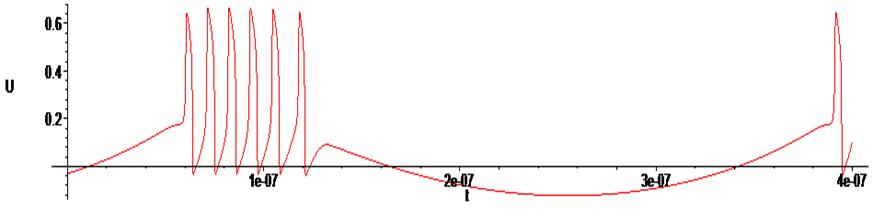
> odeplot(RsS1,[t,i(t)],0.. .4e-6, numpoints = 50000);

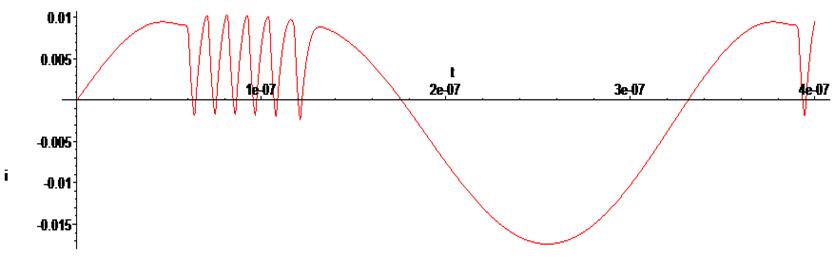
И наконец, выполним эксперимент с точно заданной ВАХ туннельного диода.

> restart: with (plots):

Warning, the name changecoords has been redefined

> DU:=diff (i(t) , t ) =  (E(t) - i(t)*R - U(t) ) / L , diff ( U(t) , t ) = ( i(t) - Idt (t) )/C ;

> Idt := (t) ->  .2854195919*U(t)*exp(-.1e2*U(t))+.115e-7*exp(20*U(t))-.115e-7 ;

> Nu := i(0) = 0 , U(0) = 0 :

> S := i(t) , U(t) :

>  R := 10: C := 1E-11: L := 1E-7:

> E:=(t) -> 0.3:  # Входной сигнал - постоянное напряжение 0.3В

> Rs := dsolve ( { DU , Nu } , {S} , type = numeric , maxfun = 1000000 ) ;

> odeplot(Rs,[t,U(t)],0.. 2.8*10^(-8), numpoints = 500);

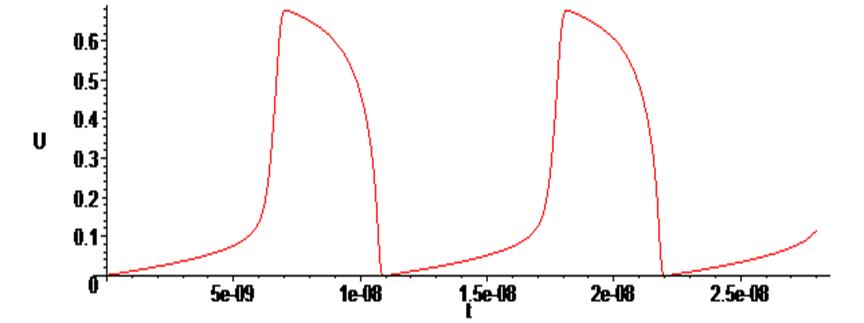
> odeplot(Rs,[t,i(t)],0.. 2.8*10^(-8), numpoints = 500);

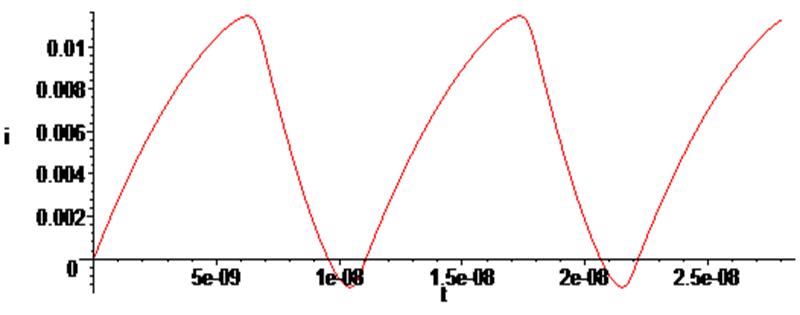
Сравним форму колебаний с результатами предыдущих экспериментов!

Далее, как и в предыдущих случаях, выполним моделирование при гармоническом входном сигнале.

> restart:

> with (plots):

Warning, the name changecoords has been redefined

> DU1:=diff (i(t) , t ) =  (E(t) - i(t)*R - U(t) ) / L , diff ( U(t) , t ) = ( i(t) - Idt (t) )/C ;

> Idt := (t) ->  .2854195919*U(t)*exp(-.1e2*U(t))+.115e-7*exp(20*U(t))-.115e-7 ;

> E:=(t) -> 0.3*sin(19000000*t):

> GE := plot(E(t), t=0 .. .4e-6):

> GE ;

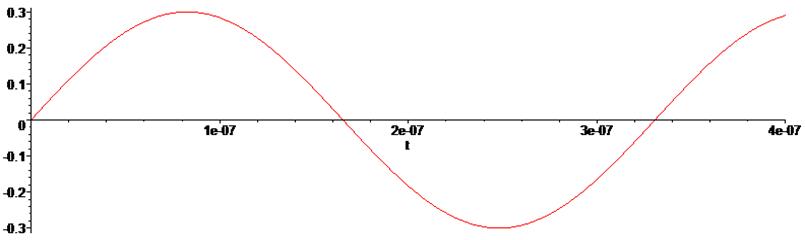
> Nu := i(0) = 0 , U(0) = 0 :

> S := i(t) , U(t) :

> R := 10: C := 1E-11: L := 1E-7:

> Rs1 := dsolve ( { DU1 , Nu } , {S} , type = numeric , maxfun = 10000000 ) ;

> GU := odeplot(Rs1,[t,U(t)],0.. .4e-6, numpoints = 50000 , color = green ):

> GU ;

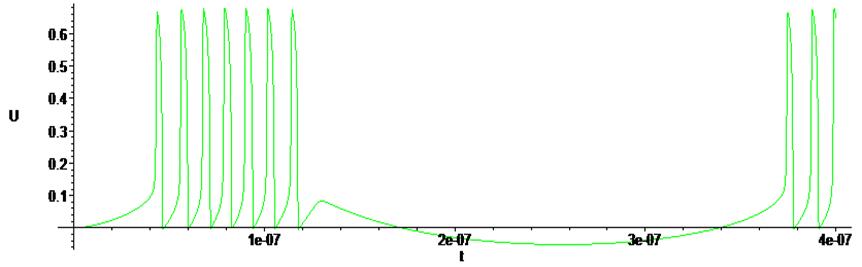
> plots [display] ( { GE, GU } ) ;

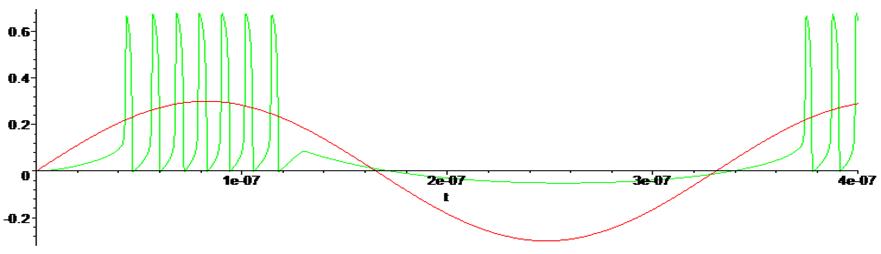
> odeplot(Rs1,[t,i(t)],0.. .4e-6, numpoints = 50000);

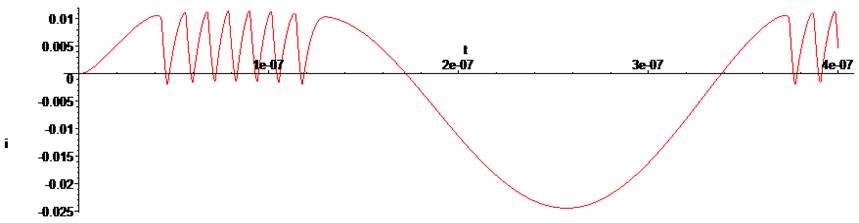
Меняя параметры цепи, например, амплитуду входного синусоидального напряжения, можно  наблюдать интересное поведение графиков изменения напряжений и токов схемы, которые сложно предсказать без проведения моделирования.

Выводы: Таким образом, вид кривой, а значит и точность экспериментальных данных и полученных аппроксимирующих кривых существенно влияет на результаты моделирования, и, соответственно, проектирования электронных и, в общем случае, любых технических систем.

В наибольшей степени данное обстоятельство играет роль при моделировании и проектировании нелинейных систем.