Линейные цепи постоянного тока

РЕСПУБЛИКА  БЕЛАРУСЬ

Белорусский Государственный Университет Транспорта

Кафедра: « Электротехника»

РАСЧЕТНО-ГРАФИЧЕСКАЯ  РАБОТА №1

Линейные цепи постоянного тока

Шифр:191

Выполнил:                                                                     Проверил:

Студент гр. ЭС-21                                                         Преподаватель

Романченко А.                                                               Волынец В.В.

2004

ЗАДАНИЕ:

В линейной электрической цепи, содержащей резисторы, катушки индуктивности и конденсаторы, действуют идеальные источники ЭДС е_k(t) = E_mk sin(ωt + ψ_k) и тока         J_k(t) = J_mk sin(ωt + α_k), где k- порядковый номер ветви.

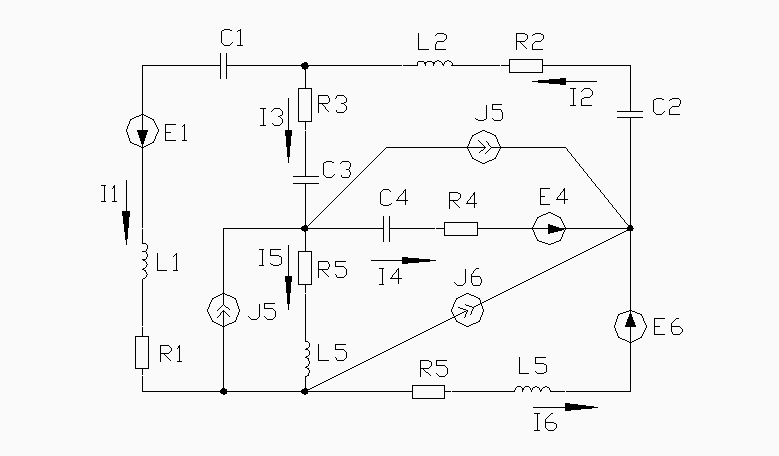Параметры пассивных элементов:

R₁ = 40 Ом           L₁ = 170 мГн              С₁ = 50 мкФ

R₂ = 50 Ом           L₂ = 190 мГн              С₂ = 45 мкФ

R₃ = 60 Ом                                              С₃ = 55 мкФ

R₄ = 45 Ом                                              С₄ = 60 мкФ

R₅ = 70 Ом           L₅ = 185 мГн 

R₆ = 30 Ом           L₆ = 220 мГн 

Параметры источников:

f = 150

E_m1 = 120             ψ₁ = 30º          

E_m4 = 140              ψ₄ = 30º           J_m4 = 2             α₄ = 25º

                                                     J_m5 = 3             α₅ = 30º

E_m6 = 165             ψ₆ = 40º           J_m6 = 4             α₆ = -20º

Для заданной схемы :

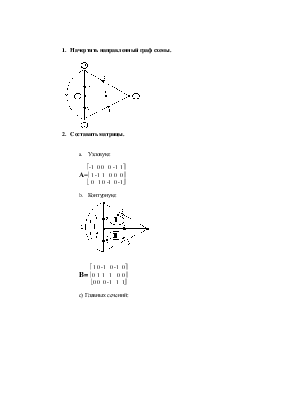
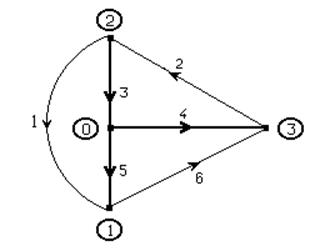
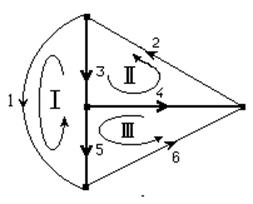
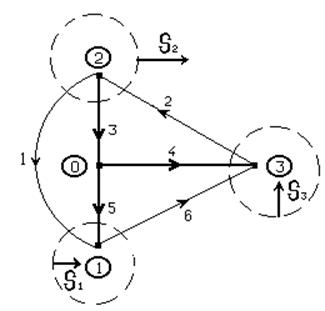
1.  Начертить направленный граф схемы, указать на нем дерево и связи.

2.  Составить матрицы: узловую, контурную и главных сечений.

3.  Вычислить комплексные сопротивления ветвей.

4.  Записать матрицы действующих значений ЭДС источников ЭДС и токов источников тока в комплексной форме.

5.  Рассчитать токи в ветвях схемы методом контурных токов.

6.  построить топографическую векторную диаграмму напряжений для всех элементов одного из контуров, содержащего 2 или 3 источника ЭДС.

1. Начертить направленный граф схемы.

2. Составить матрицы.

1. Узловую:

é-1  0 0   0 -1  1ù

А=ê 1 -1 1   0  0  0ú 

ë 0   1 0 -1  0 -1û

2. Контурную:

é1 0 -1   0 -1  0ù

B= ê0 1  1   1   0  0ú

ë0 0  0 -1   1  1û

с) Главных сечений:

é-1  0 0   0 -1  1ù

Q=ê 1 -1 1   0  0  0ú 

ë 0   1 0 -1  0 -1û

3. Вычислить комплексные сопротивления ветвей.

  w= 2 p f = 924.478  Гц

Z₁ = R₁ + j (w L₁ –1 / w C₁ ) =  40 + j (942.478 * 170*10^-3- 1 / 942.478 * 50*10^-6) =

= 40 + j 139.001 Ом

Z₂ = R₂ + j ( w L₂ - 1 / w C₂ ) =  50 + j (942.478 * 190*10^-3- 1 / 942.478 * 45*10^-6) =

= 50 + j 155.492 Ом

Z₃ = R₃ + j (-1 / w C₃ ) = 60 - j ( 1 / 942.478 * 55*10^-6) = 60 – j 19.292 Ом

Z₄ = R₄ + j (-1 / w C₄ ) = 45 - j ( 1 / 942.478 * 60*10^-6) = 45 – j 17.684 Ом

Z₅ = R₅ +j w L₅ = 70 + j (942.478 * 185*10^-3) = 70 + j 174.358 Ом

Z₆ = R₆ + j w L₆ = 30 + j (942.478 * 185*10^-3) = 30 + j 207.345 Ом

4. Записать матрицы действующих значений ЭДС и токов источников тока в комплексной форме.

E₁=(120 / Ö2) е^j60°= 42.43 + j 73.48  B

E₁=(140 / Ö2) е^j30°= 85.73 + j 49.49 B

E₁=(165 / Ö2) е^j40°= 89.37 + j 74.99 B

J₄=(2 / Ö2) е^{j 25°}= 1.28 + j 0.59 A

J₅=(3 / Ö2) е^{j 30°}= 1.84 + j 1.06 A

J₆=(4 / Ö2) е^{-j 20°}= 2.66 – j 0.97 A

 é42.43 + j 73.48ù

                                               ½          0            ½

E^(В)=[ E₁, 0, 0, E₄, 0, E₆]^T=    ½          0            ½

                                   ½85.73 + j 49.49½

                                   ½          0            ½

                                    ë89.37 + j 74.99û

 é        0           ù

                                               ½        0           ½

J^(В)=[0, 0, 0, -J₄, J₅, -J₆]^T=      ½        0           ½

                                   ½1.28 + j 0.59 ½

                                   ½1.84 + j 1.06 ½

                                    ë2.66 – j 0.97 û

5. Рассчитать токи в ветвях схемы методом контурных токов.

Запишем контурные уравнения в матричной форме:

B * Z^(B)* B^T * I^(K) = B * E^(B) -  B * Z^(B) * J^(B)  ,

Где:

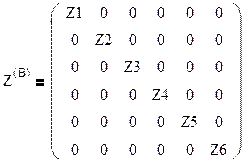
Подставив значения получаем:

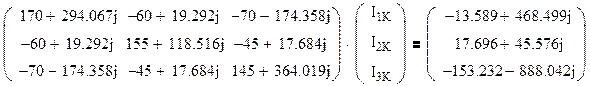
Найдем контурные токи по формулам Крамера:

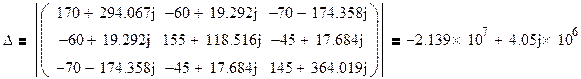
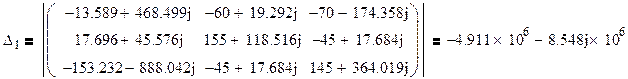
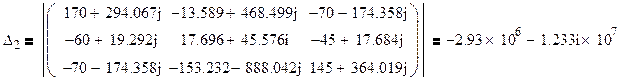
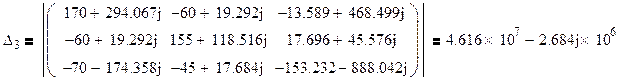
Получаем :

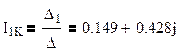
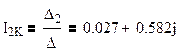
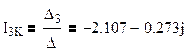
Найдем токи в ветвях схемы по формуле:

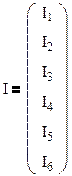
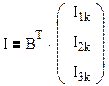
, где

Подставив значения получаем:

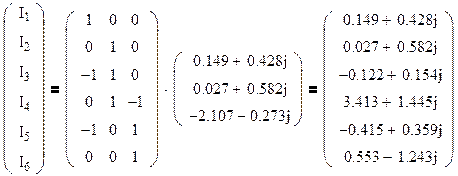
Составим баланс электрических мощностей:

S_ист = Ĭ₁ E₁ + Ĭ₄ E₄ + Ĭ₆ E₆ - Ĵ₄ U₄ + Ĵ₅ U₅ - Ĵ ₆ U₆  =

⁼

­-

= 722.177+273.873j

S_нагр = | I₁| ²· Z₁ + | I₂| ²· Z₂ + | I₃| ²· Z₃ + | I₄| ²· Z₄ + | I₅| ²· Z₅ + | I₆| ²· Z₆ =

⁼⁺

⁺