Так как считаем, что большинство случайных процессов является Гаусовскими, то для такого класса сигналов линейные фильтры также обеспечивают выделение полезной информации с требуемыми показателями.
Для фильтрации импульсных помех применяются нелинейные фильтры в которых в качестве информационного параметра используется медиана плотности распределения информации.
Методы линейной фильтрации:
1. Любую линейную динамическую систему можно представить с помощью передаточной функции импульсной или переходной характеристики.
Передаточная функция линейной системы определяется как отношение функций представляющих собой частичные спектры выходных и входных сигналов. Модуль передаточной функции есть АЧХ системы |H(w)|.
Действие фильтров определяется скоростью применения АЧХ за полосой пропускания, т.е. крутизной АЧХ.
æ=d|H(w)|dw
æ=dln|H(w)|dlg(w)
Октава –интервал частот, где частота изменяется вдвое.
Идеальный фильтр НЧ- фильтр, с полосой пропускания от 0 до w1.
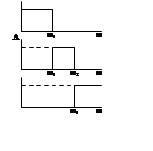 А
ФНЧ
А
ФНЧ
1
1 Полосовой
А
1 ФВЧ
Физическая реализация системы:
Фильтр может быть физически реализован, если между подачей сигнала на его входе и возникновением сигнала на выходе системы имеется связь. Т.е. сигнал на выходе не появляется раньше чем сигнал на входе.
Реакция системы на входное воздействие в виде единичного импульса типа дельта функции называется импульсной характеристикой системы.
h(t)=0 при t<0, чтобы такой фильтр реализовывался физически.
В математике это называется условием Каузальности.
2. Условие физической реализации - затухание импульсной характеристики во времени.
h(t)→0, при t→∞
Фильтр называется устойчивым, если выполняется условие абсолютной интегрируемости импульсной характеристики.
![]()
В спектральной области устойчивость факторов определяется крирерием:
![]()
Это критерий Пэливинера.
Согласно этим условиям физически неосуществим фильтр,
АЧХ-ка которого в некоторой полосе частот имеет нулевые значения.
Т.о. идеальные фильтры являются физически нереализуемыми.
Фильтры, не удовлетворяющие условиям физической осуществимости называются математическими фильтрами.
28. Цифровая фильтрация.
Цифровой фильтр представляет собой устройство, реализующее в общем случае решение уравнения в конечных разностях
![]()
где y,x – отсчёты вых. и вх. сигналов фильтра.
аi , bi – коэфф.
Если известны аi , bi , yi , xi , - и i > - N+2 можно брать любые отсчёты.
Цифровая фильтрация – точное действие, в самом цифровом фильтре за счёт округления, усечения, усреднения, полученного неточного значения.
Недостатки цифровой фильтрации:
1. Относительно низкая скорость обработки сигнала, за счёт использования устройств цифровой обработки.
2. Необходимость использования на входе и выходе АЦП и ЦАП.
3. Большая потребляемая мощность.
4. Высокая стоимость.
Цифровые фильтры, реализующие данный алгоритм, называются рекурентными . Часто этот алгоритм упрощают:
![]()
При аi = 0 Фильтр нерекурентный цифровой .
Нерекурентные фильтры называются трансверсальными. В нерекурентных фильтрах на 1 отсчёт выходного сигнала необходимо выполнить N операций умножения N-1 операций сложения.
Рекурентный фильтр – требуется меньше операций.
Вывод: Любой фильтр д.б. согласован с сигналом.
29. Измерение электрических величин.
Электромеханические измерительные механизмы и приборы.
Структура электромеханического прибора:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.