Дискретизация и восстановление непрерывных функций. Кодирование измерительной информации. Общие вопросы фильтрации измерительных сигналов. Измерение электрических величин, страница 2

1.  обнаружение детерминированного сигнала известной формы на фоне помех.

2.  Оценка информативных параметров квазидетерминирован­ного сигнала, наблюдаемого на фоне помех.

Фильтрация случайных сигналов.

1.  обнаружение сигнала — задачи фильтрации в этом случае состоит в обработке смеси сигнала и помехи, которая обес­печила бы максимальную вероятность правильного реше­ния относительно наличия сигнала в наблюдаемом случай­ном процессе.

Т.к. форма сигнала известна, то в этом случае нет необходимости ограничивать искажения сигнала фильтром. Поэтому в процессе фильтрации необходимо обеспечить максимально возможное превышение амплитуды сигнала над помехой, используя свой­ство сигнала и помехи. Если по предположениям случайный процесс представляет собой аддитивную смесь полезного сигнала и помехи, при этом спектр сигнала равен S(jw), а спектр плотно­сти помехи W(jw), то оптимальный фильтр, для обнаружения сигнала должен обладать следующей передаточной функцией:

где S^*( jw) — комплексно сопряжённая функция по отношению к S( jw);   t₀ — момент времени, в который отношение сиг­нал/помеха достигает максимальной величины.

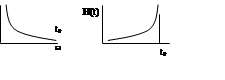Оптимальный фильтр с АЧХ вида

Хорошо пропускает частоты, на которых помеха слабая. При этом ФЧХ фильтра обеспечивает синфазность всех частот сиг­нала в момент времени t₀.

Если помеха представляет собой некоррелированный случайный процесс, т.е. типа белого шума, то с точностью до постоянного множителя передаточная функция передаточного фильтра H( jw) выражается характеристикой: H( jw) =S^*( jw).

Такой фильтр называют согласованным. Во временной коорди­нате характеристика такого сигнала

h(t)=X(t₀–t),

т.е. импульсная характеристика такого фильтра является зеркаль­ным отображением относительно момента наблюдаемого сигнала S(t).

Фильтрация квазидетерминированных сигналов.

Пусть будет сигнал X(t), а информационный параметр А. Рас­смотрим оценку параметра:        Х=А×U(t),

где U — известная функция времени, описывающая форму сигнала, наблюдаемая на фоне помехи со спектральной плотно­стью энергии W(jw). Эту задачу можно решить с помощью оптимального фильтра с передаточной характеристикой, которая совпадает с передаточной функцией фильтра обнаружения, т.к. для снижения случайной погрешности, оценки параметра А по результатам измерения выходного напряжения фильтра в момент времени t₀ необходимо добиться максимума превышения сигнала над помехой. Структура этого фильтра выглядит таким образом

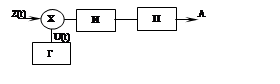
Х — перемножитель; П —преобразователь; Г — генератор; И — интегратор.

Алгоритм работы:

Z(t) — аддитивная смесь сигнала X(t) и помехи, умножается на образцовый сигнал U(t), который формируется в интервале времени от 0 до t₀. В интеграторе И подвергается линейному преобразованию. Образцовый сигнал U(t) определяет импульс­ную характеристику фильтра, должен быть согласован с формой полезного сигнала. При этом для линейной оценке параметров сигнала, наблюдаемого на фоне некоррелируемого шума, макси­мальное значение выходного сигнала фильтра достигается в момент времени t₀. При этом :

При этом коэффициент преобразования

если U(t) отличается от идеального сигнала, то точность оценки падает.

Фильтрация сложных сигналов

Если форма входных сигналов не известна, то ни один из выше названных методов не позволяет реализовать оптимальную фильтрацию. Для её реализации используются статистические критерии, обеспечивающие минимум дисперсии воспроизведения полезного сигнала. для этого необходимо априорная информация о статистических характеристиках помехи e(t) и сигнала Х(t), оба являются случайными. Выходной сигнал фильтра представляется связанным с некоторым выходным линейным преобразованием: