Анализ динамических и частотных характеристики линейных стационарных динамических систем

Лабораторная работа №7

Анализ динамических и частотных характеристики линейных стационарных динамических систем

Выполнил Громов Е.А., ЭМ-22, вариант

Цель работы: Ознакомление с динамическими и частотными характеристиками линейных стационарных динамических систем и получение навыков исследования их моделей в ControlSystemToolbox.

 1. Постановка задачи

В качестве объекта исследования выступают линейные (линеаризованные) динамические стационарные ТС с одним входом и одним выходом. При этом модель одномерной технической ТС (ТС) задана в виде комплексной передаточной функции, записанной как отношение полиномов

.

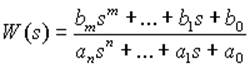Необходимо:

1. Определить полюса и нули передаточной функции

, .

2. Записать дифференциальное уравнение, определяющее функционирование ТС.
3. Построить графики переходной и импульсной функции:

h(t), w(t).

4. Построить логарифмические частотные характеристики

L (w ).

5. Построить частотный годограф Найквиста

W(iw), w = [0, ¥ ].

6. Представить исходную систему в виде последовательного соединения типовых звеньев. Построить характеристики этих типовых звеньев.
7. Получить передаточные функции ТС при последовательном и параллельном соединении звеньев с указанными передаточными функциями.
8. Получить передаточную функцию звена, охваченного различными видами отрицательной обратной связью. Построить графики переходной и импульсной функции, а также логарифмические частотные характеристики для одного из видов обратной связи (выбрать самостоятельно).

Задана передаточная функция ТС

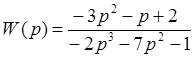
Листинг программы:

% Создаю LTI-объект с именем w

w=tf([-3 -1 2],[-2 -7 0 -1])

% Нахожу полюса передаточной функции

pole(w)

% Нахожу нули передаточной функции

zero(w)

% Строю график переходной функции

step(w)

% Строю график импульсной переходной функции

impulse(w)

% Строю диаграмму Боде

bode(w)

% Строю частотный годограф Найквиста

nyquist(w)

% Выполняю построение последних четырёх графиков в LTI-viewer

ltiview(w)

Результаты расчёта:

Transfer function:

  3 s^2 + s - 2

-----------------

2 s^3 + 7 s^2 + 1

Полюса функции

ans =

  -3.5399         

   0.0200 + 0.3753i

   0.0200 - 0.3753i

Нули функции

ans =

   -1.0000

    0.6667

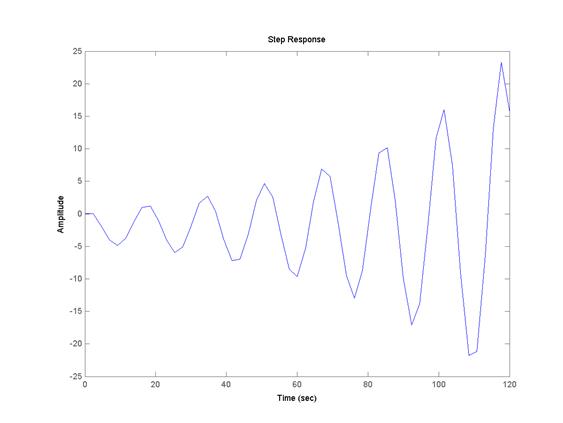
Переходная функция h(t).

Построим импульсную переходную функцию командой impulse(w).

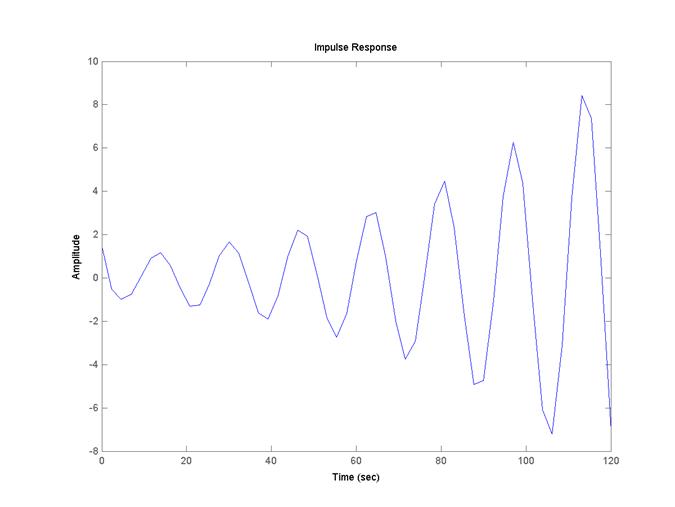
Импульсная переходная функция.

Диаграмму Боде получаю, используя команду bode(w)

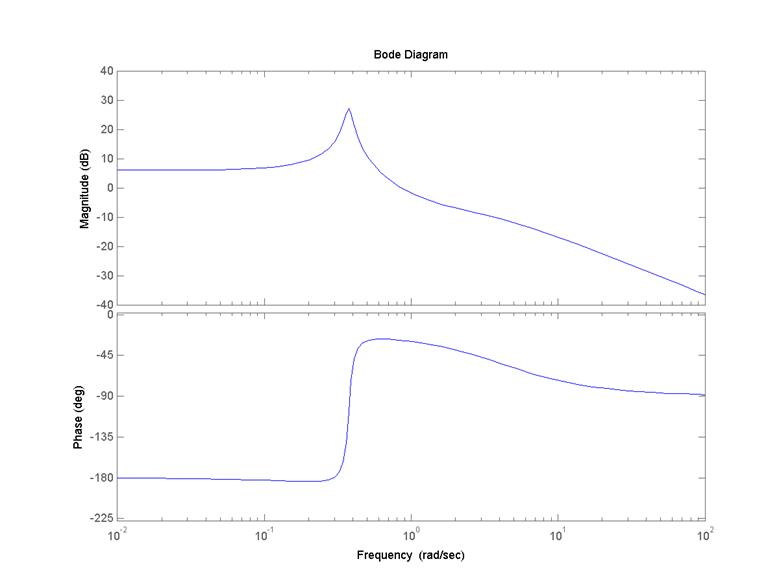
Логарифмические частотные характеристики.

Определяю частотный годограф Найквиста, выполнив команду nyquist(w)

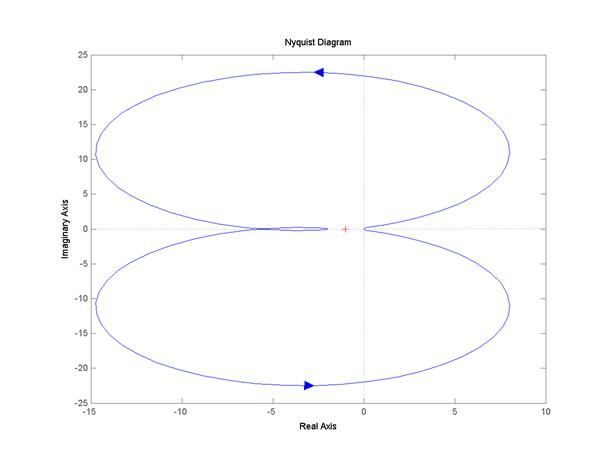
Частотный годограф.

LTI-viewer.

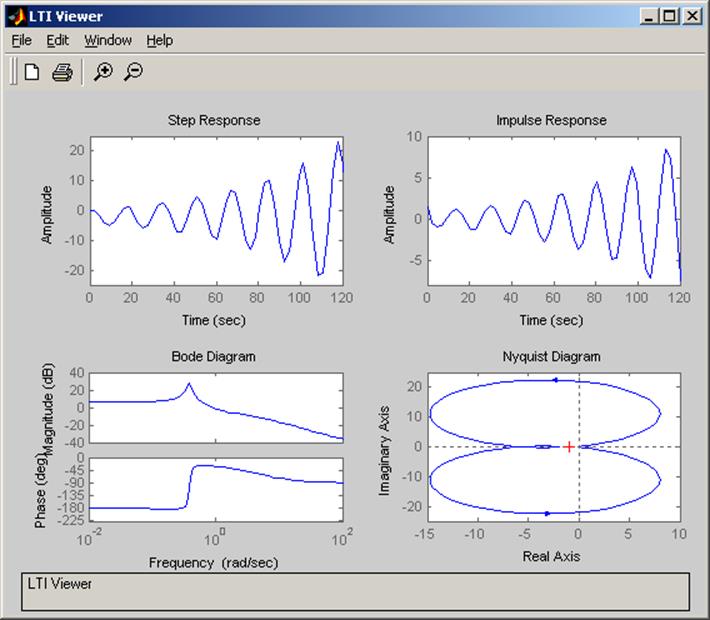Последовательное соединение

>> w=tf([-3 -1 2],[-2 -7 0 -1])

 Transfer function:

  3 s^2 + s - 2

-----------------

2 s^3 + 7 s^2 + 1

>> w1=w

Transfer function:

  3 s^2 + s - 2

-----------------

2 s^3 + 7 s^2 + 1

>> w2=w

Transfer function:

  3 s^2 + s - 2

-----------------

2 s^3 + 7 s^2 + 1

>> w=series(w1,w2)

Transfer function:

      9 s^4 + 6 s^3 - 11 s^2 - 4 s + 4

--------------------------------------------

4 s^6 + 28 s^5 + 49 s^4 + 4 s^3 + 14 s^2 + 1

ltiview(w)

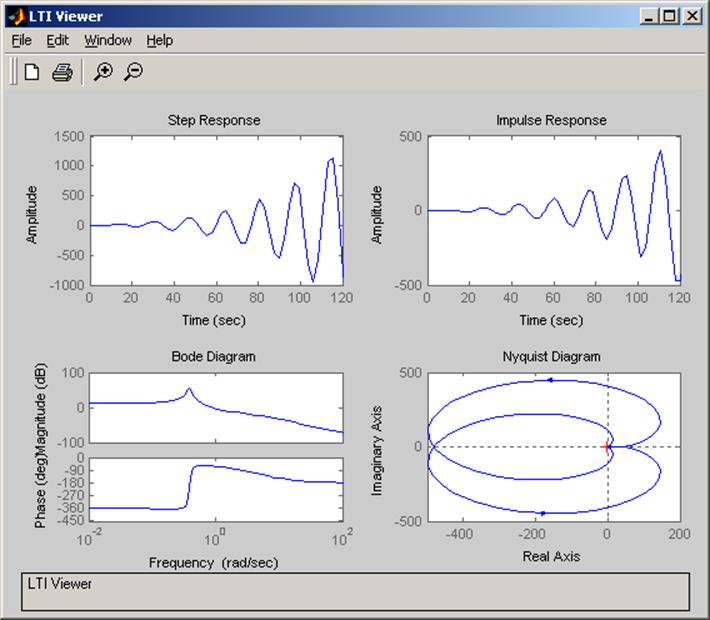Параллельное соединение

w=tf([-3 -1 2],[-2 -7 0 -1])

Transfer function:

  3 s^2 + s - 2

-----------------

2 s^3 + 7 s^2 + 1

w1=w

Transfer function:

  3 s^2 + s - 2

-----------------

2 s^3 + 7 s^2 + 1

w2=w

Transfer function:

  3 s^2 + s - 2

-----------------

2 s^3 + 7 s^2 + 1

>> w=parallel(w1,w2)

Transfer function:

12 s^5 + 46 s^4 + 6 s^3 - 22 s^2 + 2 s - 4

----------------------------------------

4 s^6 + 28 s^5 + 49 s^4 + 4 s^3 + 14 s^2 + 1

ltiview(w)

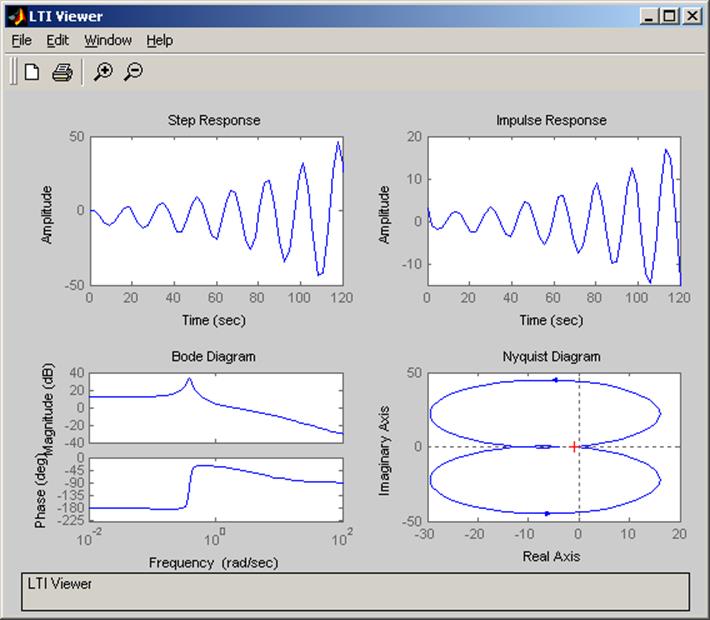
Вывод: Впроцессе выполнения данной лабораторной работы я ознакомился с динамическими и частотными характеристиками линейных стационарных динамических систем и получил навыки исследования их моделей в Control System Toolbox.