Теория электрических цепей: Руководство к лабораторным работам, страница 8

Следует заметить, что несмотря на то, что расчет по уравнениям Кирхгофа про-  водят редко, писать уравнения по законам Кирхгофа надо уметь обязательно.

 При расчете цепей наиболее часто используют 2 метода: метод контурных токов и метод узловых потенциалов. На выбор того или другого метода влияет много обсто-

ятельств. Лучше владеть и тем и другим. Число уравнении по методу контурных токов равно числу уравнении по 2-ому закону Кирхгофа и равно: N₂=В-( У-1). Есть особенность, связанная с наличием ветвей с источниками тока. Такие ветви создают с любыми другими ветвями свой контур с известными контурными токами.

Для схемы по рис.1.14 получаем: надо составить 2 уравнения: 2=5-(4-1). А ветвь

с источником тока (J₆) создаст известный контурный ток (I₃₃), который протекает по сопротивлениям R₃, R₄ и источнику тока. Будем считать, что в 1-ом контуре протекает контурный ток  I₁₁, а во 2-ом контуре контурный ток  I₂₂.

Число уравнений по методу узловых потенциалов равно числу уравнении по 1-ому закону Кирхгофа и равно: У-1.При этом потенциал одного ( в принципе любого) узла можно считать равным 0. Для схемы по рис.1.14 лучше принять потенциал узла 4 за ноль. Т.е φ₄=0. Тогда, учитывая, что внутреннее сопротивление источника Е₂ равно 0, а следовательно по закону Ома нет падения потенциала на внутреннем сопротивлении, можно утверждать, что потенциал узла 3 равен Е₂. Т.е φ₃= Е₂.

Студент! Это достойно особого внимания. Но, тогда надо составить только два уравнения. Записанные уравнения по данным методам сведем в таб.1.5

                                                                                                                      Таблица 1.5

Метод контурных токов		Метод узловых потенциалов
1-ый кон	I11 (RE+R3+R5)- I22 R5 =E1-J6 R3	1-ый узел
2-ой кон	-I11R5- I22 (R4+ R5)+J6R4=-E2	2-ой узел

Решив систему уравнений по методу контурных токов, найдем неизвестные контурные токи: I₁₁ и I₂₂ и токи в ветвях: I₁= I₁₁; I₂=- I₂₂; I₃= I₁₁+J; I₄= I₂₂+J; I₅= I₁₁- I₂₂.

Решив систему уравнений по методу узловых потенциалов, найдем неизвестные                

потенциалы: φ₁ и φ₂ . А затем токи в ветвях, используя закон Ома.

Обратите внимание на выражение для тока: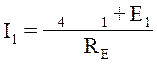 . Здесь использован закон Ома, для ветви, где имеется э.д.с. Выражения для других токов приведены в таб.1.6

                                                                                                                 Таблица 1.6

Для расчета I₂ использован 1-ый закон Кирхгофа. Почему?

Сделаем еще одно важное с практической точки замечание. Очень часто необходимо знать разность потенциалов между какими-то 2-мя точками. Это можно сделать 3-мя способами:

1. взять реальную схему и вольтметром произвести измерение.

2. если  известны потенциалы в схеме, то найти соответствующую разность

R3

3. использовать 2-ой закон Кирхгофа. Пусть нас интересует разность потенциалов между узлом 2 и точкой а на рис.1.14. Для наглядности на рис.1.15 выделен фрагмент

                                3              схемы. Будем считать, что токи I₁ и I₅ известны. Техноло- 

I5

                                           гия действий такова: Выбираем направление искомого на-

             U_3а                           пряжения- U_3а. Выбираем направление обхода вспомогат-

I1

RE

а

                                                ельного контура. Записываем уравнение по 2-ому закону