Применение операционного усилителя для выполнения математических операций, страница 3

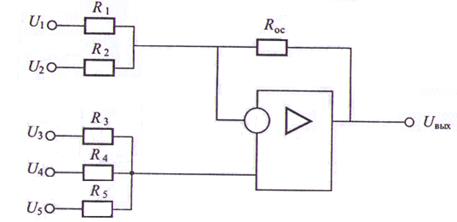
Рис. 8. Схема суммирования (к задаче 7)

Задача 8. Определить сопротивление R₁в схеме, изображенной на рис. 9, если U₁ = 2 В; U₂ = -2 В; U₃ = 4 В; R_ОС = R₂ = R₃ = 2 кОм; U_ВЫХ = -4 В.

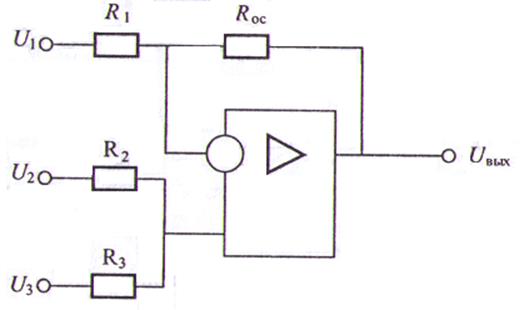
Рис. 9. Схема суммирования (к задаче 8)

4. Интегрирование сигналов с помощью операционных усилителей

Простейшая схема интегратора на операционном усилителе представле­на на рис. 10. В цепи отрицательной обратной связи стоит интегрирующий элемент — емкость.

При решении задач, как в части 1, будем полагать, что входными токами ОУ можно пренебречь, а дифференциальное входное напряжение опреде­ляется формулой (10). Тогда основные уравнения можно записать в виде

I +I_ОС = I_ВХ.ИН.                                                                                 (29)

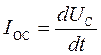,                                                            (30)

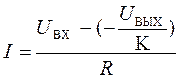,                                                      (31)

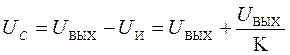,                                           (32)

Подставив в уравнение (30) выражения (29), (31) и (32), получим

  

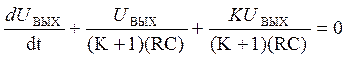
или, после интегрирования

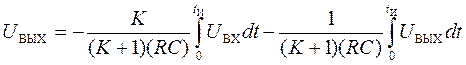,                      (33)

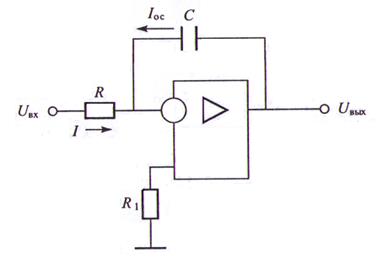
Рис. 10. Схема интегратора на операционном усилителе

    Здесь t_И— время интегрирования. Выражение (4.33) справедливо, если в момент t= 0 конденсатор разряжен. Если конденсатор в начальный мо­мент заряжен, то к выражению (33) нужно добавить начальное напряже­ние конденсатора.

    Первое слагаемое в правой части (33) дает результат интегрирования входного сигнала, а второе — ошибку, связанную с тем, что коэффициент усиления реального операционного усилителя не бесконечен. Если усили­тель — идеальный, то и второе слагаемое исчезает:

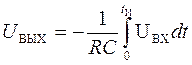,                                                    (34)

Если входной сигнал не зависит от времени, то уравнение (4.33) можно решить аналитически:

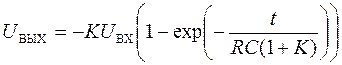.                                     (35)

Если время интегрирования t_Имного меньше , а К >>1, то с хорошей точностью

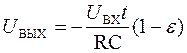.                                                     (36)

где

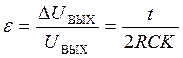.                                                     (37)

-относительная ошибка интегрирования. Оценкой (37) для ошибки ин­тегрирования можно пользоваться и при интегрировании функций  U_ВХ (t), зависящих от времени.

   Кроме ошибки, связанной с конечностью коэффициента усиления ОУ, при интегрировании возникают ошибки, связанные с наличием входных токов усилителя и с напряжением смещения. Погрешность из-за входных токов можно ликвидировать, если уравнять сопротивления на входах усили­теля, т. е. в схеме рис. 10 принять R = R₁. Однако из-за разности входных токов возникает погрешность, которую можно оценить по формуле        

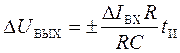,                                                    (38)

Погрешность, связанная с напря­жением смещения, оценивается по формуле

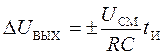.                                                     (38)

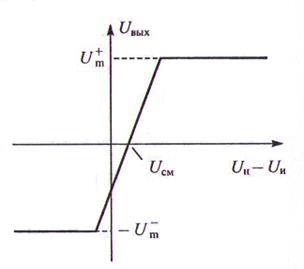
Рис. 11. Передаточная характери­стика операционного усилителя

   Из формул (37)-(39) видно, что погрешность интегрирования рас­тет с увеличением времени интегри­рования.

   Длительное интегрирование невозможно еще и потому, что выходное напряжение операционного усилителя ограничено. Это видно из характери­стики ОУ, изображенной на рис. 11. Если входной сигнал не меняет знак, то в некоторый момент времени t_И..MAX U_ВЫХдостигнет своего граничного значения и интегрирование прекратится. Допустим, что на вход усилителя подан постоянный во времени входной сигнал U_ВХ. Считая усилитель иде­альным (), и пренебрегая малым напряжением смещения U_СМ, получим из формулы (36)

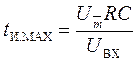
ЗАДАЧИ

Задача 9. Определить функцию U_BЫX(t), если на вход интегратора (рис. 10) подается сигнал U_BX(t) = U₀ sin(t). R = R₁ = 10 кОм, С = = 1 мкФ, Uo = 1,5 В, = 300. В начальный момент конденсатор разряжен. Усилитель считать идеальным.

Решение. Согласно формуле (34),

.

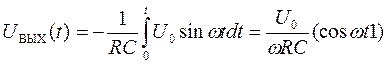Подставляя численные значения, получим:

В.

Время tследует выразить в секундах.

Задача 10. Изобразить графически результат интегрирования на идеальном интеграторе (рис.10), если R = R₁ = 20 кОм, С = 1 мкФ, а входной сигнал можно представить в виде графика (рис.12). Макси­мальное выходное напряжение ОУ равно ±10 В.

Решение. Представим первый отрезок ломаной линии рис. 12 ана­литически: U_BX =2 - kt, где к = 20 В/с, время t выражено в секундах.

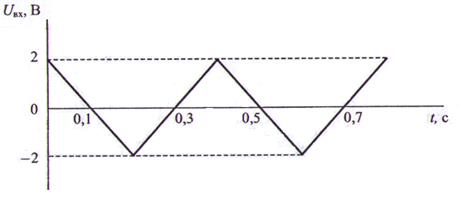
Рис. 12. Напряжение на входе интегратора (к задаче 10)

   Напряжение на выходе ОУ при t_И < 0,2 с можно определить согласно формуле (4.34), где U_BЫX выражено в вольтах, a t в секундах:

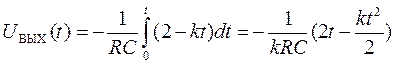
Постоянная времени RC = 20 кОм • 1 мкФ = 0,02 с. Таким образом функция U_BЫX(t) представляет собой параболу

U_BЫХ (t) = 100 (5t² - t) В.