Практический курс теоретических основ электротехники: Методическое руководство (Раздел IX-X: Расчет цепей с взаимной индуктивностью. Круговые диаграммы)

IX. РАСЧЕТ ЦЕПЕЙ С ВЗАИМНОЙ

ИНДУКТИВНОСТЬЮ

Основные вопросы

1.  Определение напряжения на катушке, индуктивно связанной с другими катушками цепи.

2.  Учет знака напряжения взаимоиндукции в уравнениях баланса напряжения?

3.  Методы расчета цепей с взаимной индуктивностью. 

4.  Эквивалентная замена индуктивных связей («развязка»).

5.  Баланс реактивных мощностей в цепях с взаимной индуктивностью.

Литература

1.  1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. – М., 1989. – § 6.1, 6.5, 6.6, 6.8.

2.  Поливанов К.М. Теоретические основы электротехники. – М., 1965. –
Ч. 1. – Гл. 6.

Примеры

Задача 1

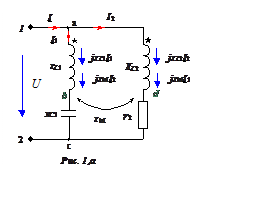В цепи, представленной на рис. 1,а

U = 120 B;

х_L1 = х_C1 = 10 Ом;

х_L2 = 8 Ом; х_М = 8 Ом;

r₂ = 8 Ом.

Найти токи I, I₁, I₂.

Построить топографическую диаграмму напря-жений.

Решение

Расчет проводится на основании законов Кирхгофа.

1. Выбираем положительные направления токов I, I₁, I₂ (рис. 1,а).

2. В соответствии с направлениями токов I₁ и I₂ включение катушек L₁ и L₂ согласное.

(На схеме показаны направления напряжений самоиндукции и взаимоиндукции в соответствии с включением и выбранным направлением токов в катушках.)

3. Расчетные уравнения по первому и второму законам Кирхгофа

I -I₁ – I₂ = 0;

jx_L1I₁+jx_M I₂ + (- jx_c) I₁ = U  (для контура 1-а-b-c-1^’);

r₂ I₂ + jx_L2 I₂ + jx_M I₁ = U.  (для контурa 1-a-d-c-1^’)

или после подстановки числовых значений

 

I -I₁ - I₂ = 0;

j10×I₁ + j8×I₂ + (– j10)×I₁ = 120;

8×I₂ + j8×I₂ + j8×I₁ = 120.

4. Из решения системы уравнений следует:

I₁ = 15 A;

I₂ = -j15 A;

I = 21,15Ð-45° A.

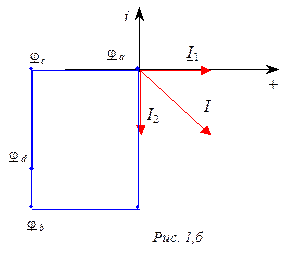5. Топографическая диаграмма (рис. 1,б).

Потенциалы точек схе-мы при допущении, что
j _a = 0:

j _b = j _a – jx_L1 I₁ – jx_м I₂ = 0 – j10×15 – j8×(-j15) =

    = (-j150 – 120) B.

j _c = j _b – (– jx_c )I₁ =

= –j150 – 120 + j150 =

= –120 B.

j _d= j _a – jx_L2 ×I_{2 –} jx_м I₁ = = –120 – j120 B.

Проверка:             j _c = j _d– r₂ ×I₂ = -120 B.

          j _a = j _c + U = 0

Задача 2

Цепь, изображенная на схеме рис. 2,а, подключена к напряжению U = 120 В, частота w = 1000 (1/c). Параметры элементов цепи:

L₁ = 0,05 Г;  L₂ = 0,04 Г;

L₃ = 0,01 Г;  C = 10 мкФ;

М₁₂ = 0,01 Г;  М₁₄ = 0,08 Г;

М₂₄ = 0,06 Г.

Активным сопротивлением катушек можно пренебречь. Определить показание вольтметра

(R_V = ∞).

Решение

1. Поскольку сопротивление вольтметра бесконечно велико, напряжение на его зажимах определится только ЭДС взаимной индукции

Е_М14 = jwМ₁₄ I₁   и   Е_М24 = jwМ₂₄ I₂.

Для определения показания вольтметра, необходимо предварительно оценить характер включения катушек L₁, L₂, L₄  и рассчитать токи I₁ и I₂  в них.

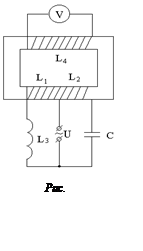
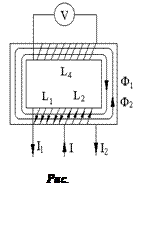При заданной конструкции устройства, токи I₁  и I₂ в катушках L₁ и L₂ создают магнитные потоки Ф₁ и Ф₂, направленные встречно (рис. 2,б). Следовательно, ЭДС самоиндукции и взаимоиндукции в этих катушках будут противоположны по знаку (катушки L₁ и L₂ включены встречно). Противоположными по знаку будут и наведенные пото-ками Ф₁ и Ф₂ ЭДС взаимной индукции в катушке L₄.

2. Расчет токов в катушках L₁ и L₂ проводится на осно-вании второго закона Кирхгофа:

			Рис. 2,б
	Рис. 2,а

 

Рис. 2,а

U= jwL₁İ₁ + jwL₃I₁ – jwМ₁₂I₂,

U = jwL₂I₂ – j(1/ wC) I₂ – jwМ₁₂I₁.

После подстановки числовых значений и решения системы уравнений

120 = j60İ₁ – j10İ₂,

120 = -j60İ₂ – j10İ₁,

имеем: I₁  = -j1,62 A,  I₂  = j2,27 A.

3. Напряжение на зажимах вольтметра определится соотношением:

U_V = | jwМ₁₄I₁ – jwМ₂₄I₂ | = |80I₁ – 60I₂| = 266 В.

Ответ: U_V = 266 B.

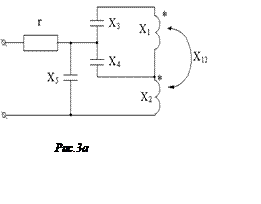Задача 3

Дано:

x₁ = 60 Ом;  x₂ = 40 Ом;

x₄ = 40 Ом;  x₅ = 50 Ом;

r = 15 Ом,  x₁₂ = 20 Ом.

Рис. 3,а

Найти x₃, при котором цепь, представленная на
рис. 3,а, находится в режиме резонанса токов.

Решение

1. Для реализации условия резонанса токов

Im(Y_вх) = 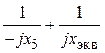= 0,

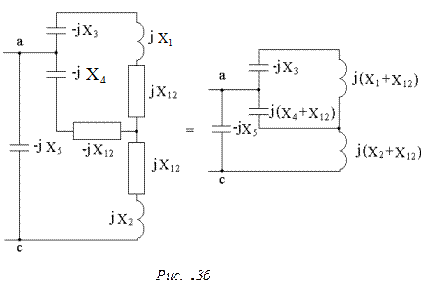
целесообразно предварительно заменить индуктивно связанные катушки x₁ и x₂ эквивалентной схемой без взаимной индуктивности (сделать «развязку» индуктивных связей) и затем найти сопротивление jx_экв участка цепи, параллельного ветви с эле-ментом Х₅.

2. Эквивалентная схема после «развязки» индуктивной связи представлена на рис. 3,б.

3. В соответствии со схемой рис. 3,б

=

=

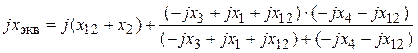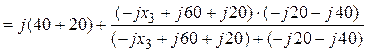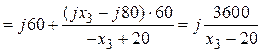 Ом.

Рис. 3,б

4. Из условия резонанса токов

=

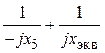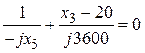
следует

х₃ = 92 Ом.

Задачи для самостоятельного решения.

Задача 4

Записать уравнения для контурных токов I₁ и I₂.

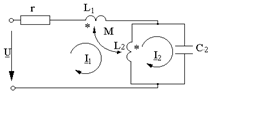Ответ:

U = I₁ [r + jw(L₁ + L₂ +2M)] –
-I₂ jw(L₂ +M),

0 = I₂ (jwL₂ -j) –

Рис. 4

Рис. 4

- I₁ jw(L₂ +M).

Задача 5

Построить векторную диаграмму токов и напряжений.

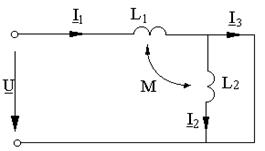Ответ: