Последовательности независимых событий и величин. Неравенство Чебышева. Типы сходимости, страница 3

Теорема 6¢.  Если – последовательность независимых  одинаково распределенных с. величин, для которых  конечны, n=1,2,…, то с вероятностью 1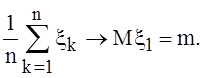

          Если же величины  не имеют конечного математического ожидания, то последовательность 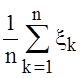с   вероятностью 1 не ограничена.

Доказательство.   Пусть 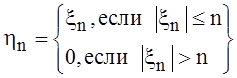, n = 1, 2, …  Так как

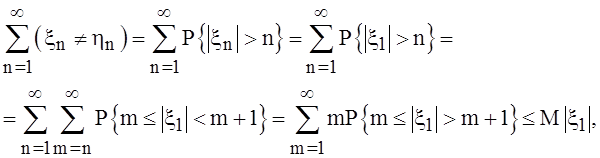
то по теореме Бореля – Кантелли событие происходит лишь конечное число раз следовательно с вероятностью 1 можно утверждать что начиная с некоторого номера . Следовательно,  

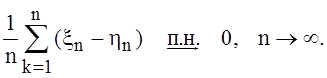
Далее, используя следствие из теоремы 4¢, имеем 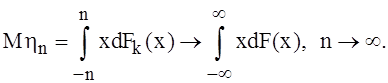 Следовательно,

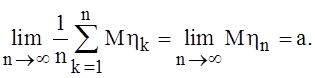
Далее, имеем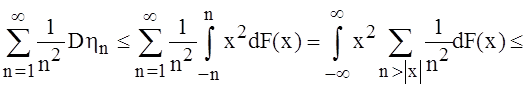

.

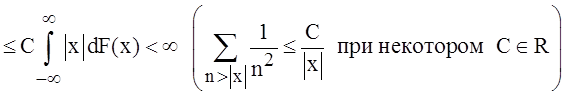Тем самым мы показали, что для последовательности  выполнено условие теоремы 6. Следовательно, имеет место сходимость почти наверное 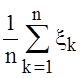к a , Теорема доказана.

Обе теоремы принадлежат А.Н.Колмогорову.

4.7  Центральная предельная теорема

Постановка задачи, решаемой центральной предельной теоремой, имеет длинную историю : от Муавра (1718 г.) и  Лапласа (1812 г.) до Ляпунова (1901 г.) и Линдеберга (1922 г.).  В трудах двух последних ученых найдены необходимые и достаточные условия сходимости       закона распределения суммы независимых с. величин к нормальному закону.  Исследования по центральной предельной теореме продолжаются до сих пор.

Термин “центральная предельная теорема” в ТВ означает любое утверждение о том, что при выполнении определенных условий функция распределения суммы индивидуально малых случайных величин с ростом числа слагаемых сходится к нормальной функции распределения.

Основную роль в этих теоремах играет теорема о связи сходимости последовательности функций распределения со сходимостью последовательности соответствующих характеристических функций – теорема непрерывности.

Теорема 8 (теорема непрерывности). Последовательность функций распределения  слабо сходится к функции распределения  тогда и только тогда, когда последовательность их характеристических функций  сходится к непрерывной предельной функции  При этом  есть характеристическая функция для  и сходимость  к  равномерная в каждом конечном интервале.

Теорема 9 (центральная предельная теорема). Пусть – последовательность независимых одинаково распределенных с. величин с  и   Тогда 

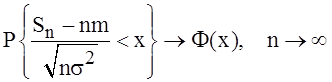,                                              (4.6)

где Ф(x) – функция нормального стандартного распределения.

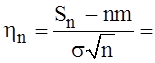
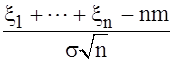Доказательство.  Функция  - непрерывная, сходимость к ней последовательности функций распределения с. величин   является сходимостью по распределению с. величин  Следовательно, мы можем воспользоваться теоремой 8. Обозначим через характеристическую функцию с. величины , n=1, 2, … , а через  - характеристическую функцию с. величины 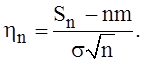 Воспользуемся свойствами 7 и 8 характеристических функций: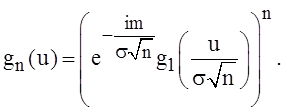 

По свойству 5 характеристических функций  дифференцируема дважды, тогда функцию 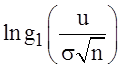 можно разложить в ряд Маклорена:

.

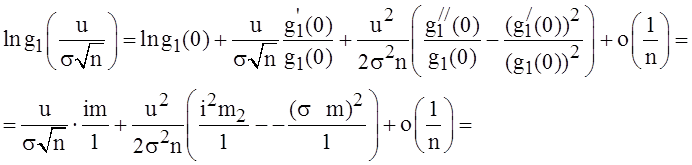
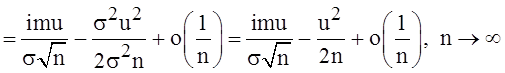Но тогда: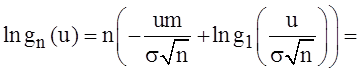

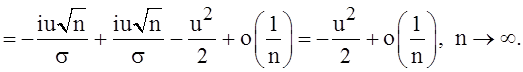
Следовательно, при  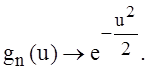 Но 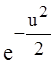– характеристическая функция стандартного нормального распределения. Теорема доказана.

Пример 3. Рассмотрим в качестве - число наступлений  некоторого события  в серии из n независимых испытаний, в каждом из которых событие наступает с вероятностью р и не наступает с вероятностью q=1-p. Тогда по теореме 9 для функций  распределения F(x) нормированного отклонения от среднего числа наступления события – с.величины

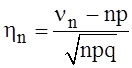  имеет место отношение  .

Это сформулированная нами ранее теорема Муавра- Лапласа.

Теорема 10 (Линдеберга). Пусть – последовательность независимых с. величин, для которых существуют  Если для всякого  выполняется условие:

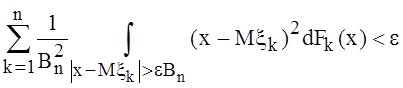                            (4.7)

где 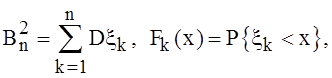 то справедливо равенство (4.6).

Действительно, не ограничивая общности рассуждений будем полагать, что  Положим 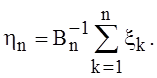 Характеристическая функция с.величины имеет вид 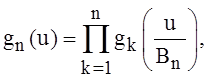 где  - характеристическая функция с. величины  Имеем