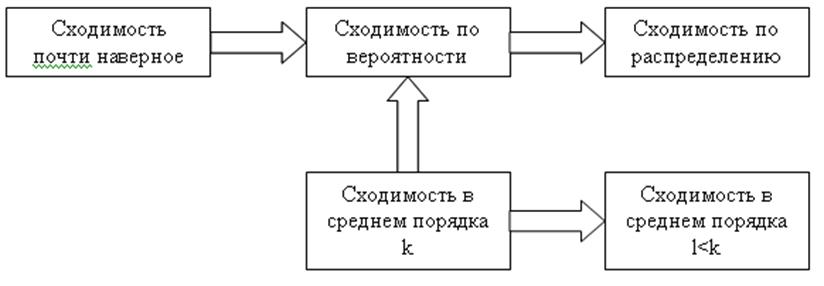
Соотношения между различными типами сходимости представлены ниже в виде схемы.
Так
называются теоремы, дающие условия, при которых арифметическое среднее с.
величин по вероятности сходится к арифметическому среднему их математических
ожиданий : 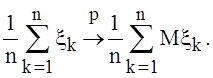
Теорема
4 (закон больших чисел). Если
последовательность независимых одинаково распределенных с. величин такова, что ![]() то
то
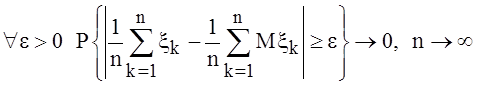 .
.
Доказательство.
Отметим прежде всего, что все ![]() одинаково распределены,
потому у них у всех одно и то же математическое ожидание и одна и та же
дисперсия. Теорема является следствием теоремы 1. Доказываемый предел можно
переписать в виде
одинаково распределены,
потому у них у всех одно и то же математическое ожидание и одна и та же
дисперсия. Теорема является следствием теоремы 1. Доказываемый предел можно
переписать в виде
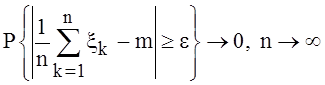 .
.
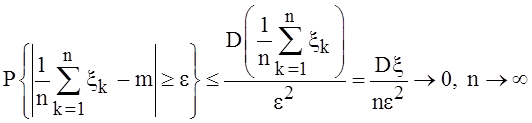 , так
как конечная сумма независимых с. величин, умноженная на число
, так
как конечная сумма независимых с. величин, умноженная на число ![]() , есть с. величина с математическим ожиданием
, есть с. величина с математическим ожиданием 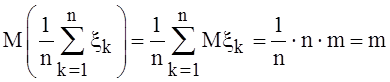 и дисперсией
и дисперсией 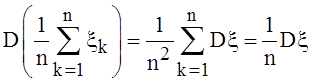 .
.
Замечание. Теорема 4 имеет место и без требования существования конечных дисперсий. Просто доказательство её будет иным.
Теорема
4¢. Если
последовательность независимых с. величин такова, что![]() существуют
и
существуют
и 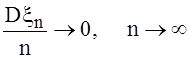 , то
, то 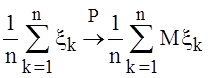 .
.
Это тоже закон больших чисел, но для произвольной последовательности с. величин, произвольной в том смысле, что не утверждается одинаковое распределение всех с. величин.
Доказательство.
Имеем 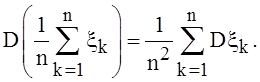 По неравенству Чебышева
По неравенству Чебышева 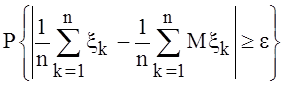
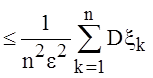 . По теореме Штольца
. По теореме Штольца 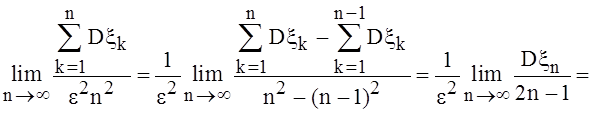
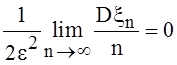 (по условию). Теорема
доказана.
(по условию). Теорема
доказана.
В основе этой теоремы лежит известная теорема Чебышева П.Л.(1880 г.):
Пусть
последовательность попарно независимых с. величин имеет математические ожидания
![]() и дисперсии
и дисперсии ![]() ,
ограниченные в совокупности числом В, то есть
,
ограниченные в совокупности числом В, то есть ![]() ,
к=1,2,3,… Тогда
,
к=1,2,3,… Тогда 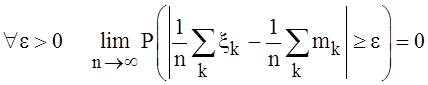 .
.
Пример
2. Пусть μ - число успехов в серии
из n независимых испытаний по схеме Бернулли, величина ![]() фиксирует успех или неудачу в
фиксирует успех или неудачу в ![]() –ом испытании по схеме Бернулли (оно
принимает значение 1 или 0 соответственно). Тогда в серии испытаний число
успехов
–ом испытании по схеме Бернулли (оно
принимает значение 1 или 0 соответственно). Тогда в серии испытаний число
успехов ![]() равно
равно 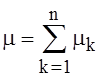 ,
, 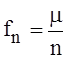 - частота успехов в nнезависимых
испытаниях. Известно, что
- частота успехов в nнезависимых
испытаниях. Известно, что ![]() .
.
По
доказанному 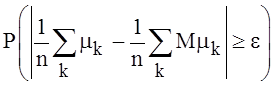 =
=![]() Последнее соотношение есть теорема Бернулли.
Последнее соотношение есть теорема Бернулли.
Ранее при определении вероятности мы говорили о приближении в каком-то смысле частот событий к вероятностям этих событий. Теперь этот смысл понятен - последовательность частот сходится к вероятности события по вероятности.
Поскольку в законе больших чисел речь идет о сходимости по вероятности среднего арифметического с. величин к некоторой постоянной величине с ростом числа n, то в каждом отдельном эксперименте (при произвольном w) закон больших чисел этой сходимости не гарантирует. А на практике мы встречаемся со с. величинами именно в отдельных экспериментах.
Усиленный закон больших чисел - это одна из форм закона больших чисел, в которой вместо сходимости по вероятности утверждается сходимость почти наверное (с вероятностью 1).
Тогда те w, для которых закон больших чисел не имеет места, образуют множество, вероятностная мера которого равна 0, т.е. он имеет место для почти всех w.
Приведем прежде всего неравенство Колмогорова:
Теорема
5. Пусть ![]() -
независимые с. величины. Если
-
независимые с. величины. Если ![]() , тогда
, тогда
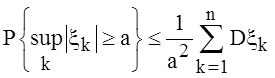 (4.5).
(4.5).
Неравенство (4.5) называют неравенством Колмогорова.
Теорема
6 (усиленный закон больших чисел).
Если ![]() – последовательность независимых с. величин, для
которых
– последовательность независимых с. величин, для
которых ![]() и ряд
и ряд
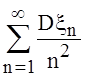 сходится, то с вероятностью 1 при
сходится, то с вероятностью 1 при ![]()
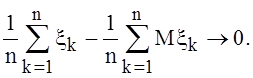
Для
доказательства теоремы нужна лемма: Если ![]() и если
и если
![]()
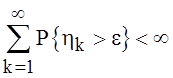 , то
, то 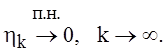
Докажем
её. Если событие ![]() обозначить
через
обозначить
через ![]() , то по теореме Бореля-Кантелли с вероятностью 1
происходит лишь конечное число событий
, то по теореме Бореля-Кантелли с вероятностью 1
происходит лишь конечное число событий ![]() . Следовательно, начиная с некоторого номера
. Следовательно, начиная с некоторого номера ![]() ,
, 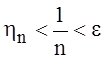 и
этот номер с вероятностью 1 существует.
и
этот номер с вероятностью 1 существует.
Доказательство
теоремы. Обозначим  Так как
Так как 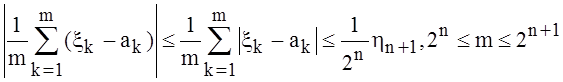 (по
свойству sup), то на основании неравенства Колмогорова
(по
свойству sup), то на основании неравенства Колмогорова 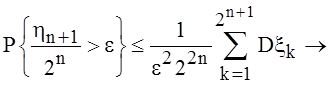
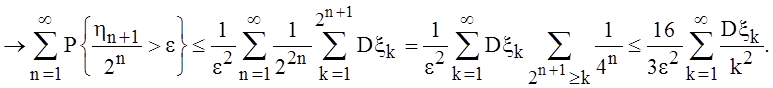 Тогда
с вероятностью 1 по лемме:
Тогда
с вероятностью 1 по лемме:
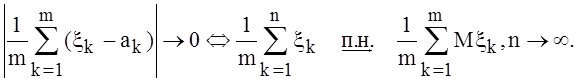
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.