Переходные процессы в нелинейных цепях

XV. Переходные процессы в нелинейных цепях

15.1. Особенности переходных процессов в нелинейных цепях

Характер переходных процессов в нелинейных цепях может существенно отличаться от характера переходных процессов в линейных цепях. Это отличие может быть как количественным, так и качественным.

Например, при подключении катушки со стальным сердечником к источнику постоянного напряжения в начальный период ток нарастает медленнее, чем у катушки без стали, а затем быстрее. При подключении такой катушки к источнику синусоидального напряжения ток в начальный период может превысить амплитуду установившегося тока в десятки раз, в то время, как в линейной R - L цепи - лишь в два раза. Это количественные отличия.

В цепях, содержащих нелинейные элементы с отрицательными параметрами на отдельных отрезках характеристик (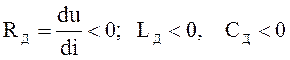), в переходных режимах могут возникать незатухающие  колебания (автоколебания) при включении цепи на постоянное напряжение, а при питании цепи от источника синусоидального напряжения могут появиться колебания напряжений и токов с частотами, отличными от частоты сети. Это качественные отличия.

Установившейся режим нелинейной цепи может зависеть от начальных условий переходного процесса, чего не бывает в линейных цепях.

Нелинейные электрические цепи в переходном режиме описываются нелинейными дифференциальными уравнениями, составленными по законам Кирхгофа. Общего аналитического метода их решения не существует. Решение нельзя представлять в виде суммы принужденных и свободных составляющих, так как в нелинейных цепях принцип наложения неприменим. Таким образом, задача расчета переходного процесса сводится к составлению и выбору способа решения нелинейного дифференциального уравнения.

Применяются приближенные методы расчета - аналитические, графоаналитические и численные. В аналитических методах нелинейные характеристики аппроксимируются аналитическими функциями. Графоаналитические методы используют графические построения, которые сопровождаются некоторыми дополнительными вычислениями. В настоящее время развитие ЭВМ позволяет использовать численные методы расчета нелинейных дифференциальных уравнений.

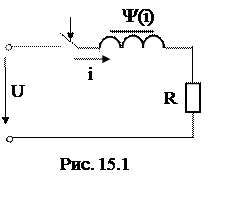
Рассмотрим применение различных методов расчета на примере схемы рис. 15.1.

15.2. Метод условной линеаризации

Переходный процесс в схеме рис. 15.1 описывается дифференциальным уравнением   .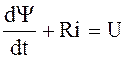

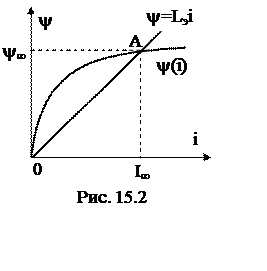
Сделаем его линейным, заменив заданную вебер-амперную характеристику  Y(i) (рис. 15.2) прямой, проведенной через начальную и конечную точки на ВбАХ. Этой прямой соответствует эквивалентная линейная индуктивность  .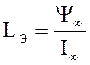

Начальная точка  Y(0)=0 и i(0)=0. Конечная точка (установившейся режим) – т. А: при t=¥ 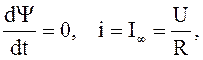     Y=Y_¥ .

тогда 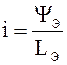  .  Получаем дифференциальное уравнение    .

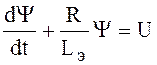Его решение 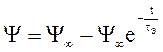   ,   где   t_э 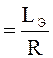  -  постоянная времени цепи.

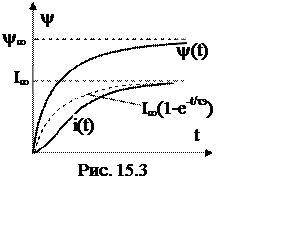
Строим  Y(t) и графически находим i(t)  (рис. 15.3).

Вначале L_диф велика, процесс нарастания тока идет медленно, затем L_диф уменьшается, и процесс ускоряется.

15.3. Метод аналитической аппроксимации нелинейной характеристики

Простейшая аппроксимация ВбАХ катушки  i=а Y². Подберем а:

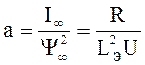,      где .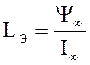

Уравнение 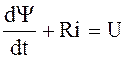    превратится в  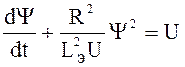- уравнение с разделяющимися переменным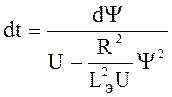и:      или   .

.

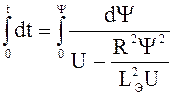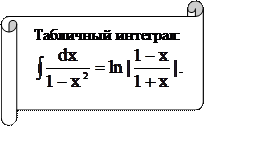
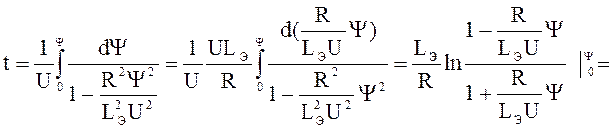
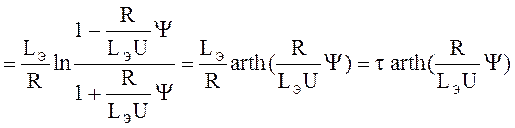Окончательно имеем: Y(t) = 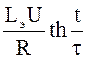;  i(t)= 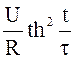, где .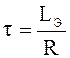

15.4. Метод кусочно-линейной аппроксимации нелинейной характеристики

Нелинейная характеристика заменяется ломаной линией, близко совпадающей с характеристикой. В результате решение нелинейного дифференциального уравнения заменяется решением совокупности линейных дифференциальных уравнений, соответствующих прямолинейным отрезкам линеаризованной характеристики.

Заменим ВАХ катушки ломаной линией 0-1-2-3, которая близко совпадает с нелинейной характеристикой Y(i) (рис. 15.4а). Зависимость дифференциальной индуктивности от тока L_диф(i) показана на рис. 15.4б.

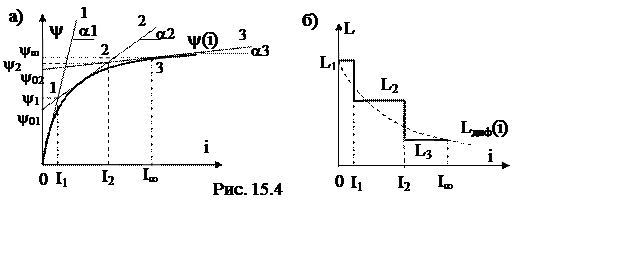Нелинейное дифференциальное уравнение 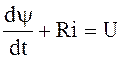   заменяется тремя линейными дифференциальными уравнениями, соответствующими отрезкам линеаризации.

Выражения  для потокосцепления на отрезках  0-1, 1-2, 2-3:       Y=L₁ i    при   0<i<I₁,

Y=Y₀₁ +  L₂ i   при   I₁<i<I₂,

Y=Y₀₂ +  L₃ i   при   I₂<i<I_¥.