Переходные процессы в нелинейных цепях, страница 2

Y₀₁ и Y₀₂ определяются пересечением продолжений отрезков 1-2 и 2-3 ломаной с осью ординат. Таким образом, 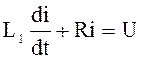                   при      0<i<I₁  и  0<t<t₁,

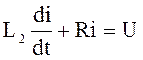          при      I₁<i<I₂  и  t₁<t<t₂,

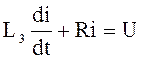          при     I₂<i<I_¥   и    t₂<t<¥.           

Обозначим  ,      ,    .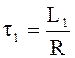

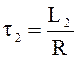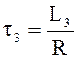Решения каждого уравнения: 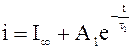      при        0<i<I₁  и  0<t<t₁,

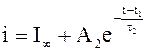                                при      I₁<i<I₂  и  t₁<t<t₂,

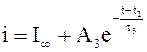                                  при     I₂<i<I_¥   и    t₂<t<¥.

Постоянные интегрирования найдем из условия невозможности скачкообразного изменения тока в точках 0, 1 и 2. Согласно первому закону коммутации i(0)=0; i(t₁)=i₁; i(t₂)=i₂.   Тогда   0= I_¥+A₁   при t=0,    I₁= I_¥+A₂  при  t= t₁,    I₂= I_¥+A₃  при  t= t₂.

Отсюда           A₁= -I_¥,            A₂= I₁-I_¥,          A₃= I₂-I_¥.

 Окончательно имеем: 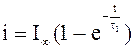        при      0<i<I₁  и  0<t<t₁,

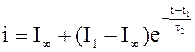         при      I₁<i<I₂  и  t₁<t<t₂,

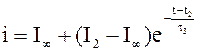          при     I₂<i<I_¥   и    t₂<t<¥.

Значения   t₁   и t₂ (припасовка) определим из услови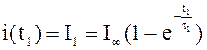й       и   .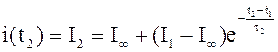

Таким образом,   t₁=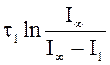,   t₂ = .

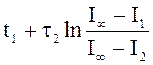График зависимости i(t) представлен на рис. 15.5.

15.5. Метод последовательных интервалов

Это численный метод расчета переходных процессов в нелинейных цепях. Суть его заключается в том, что время переходного процесса разбивают на ряд малых интервалов Dt и на каждом из них дифференциалы величин заменяют конечными приращениями. Переходя от одного интервала к следующему, получают нелинейные характеристики переходного процесса.

Рассмотрим включение катушки со стальным сердечником на постоянное напряжение U. Переходный процесс характеризуется значениями потокосцепления ψ и тока iв начале и конце каждого интервала. Величины в конце К-ого интервала обозначаем индексом K, тогда в начале К-ого или конце К-1 интервала величины имеют индекс К-1.

Дифференциальное уравнение цеп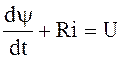и    или    .

Для К-ого интервала       Dy_K = y_K - y_K-1 » (U - R i_K-1) Dt.

В начале 1-ого интервала  t=0,  y₀=0, i₀=0,  Dy₁=UDt.    y₁=y₀ + Dy₁=UDt.

Для второго интервала   Dy₂=(U - R i₁)Dt, ,         y₂=y₁ + Dy₂.

И так далее до достижения током значения     .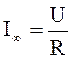

Расчет удобно выполнять в виде таблицы

K	t	iK-1	U-RiK-1	DyK	yK	iK
1	Dt	0	U	Dy1= UDt	y1=Dy1	i1
2	2Dt	i1	U-Ri1	Dy2= (U-Ri1)Dt	y2=y1 + Dy2	i2
3	3Dt	i2	U-Ri2	Dy3= (U-Ri2)Dt	y3=y2 + Dy3	i3

Очевидно,  что чем меньше интервалы Dt, тем точнее будет выполнен расчет.

В этом примере расчет выполнен методом, предложенным Эйлером. Существуют и другие методы. Например, одних методов Рунге-Кутта 4.

Недостаток этого метода, как и других численных методов, зависимость дальнейшего решения от неточности всех предыдущих значений искомой величины.

15.6. Включение катушки со сталью на синусоидальное напряжение

Дифференциальное уравнение .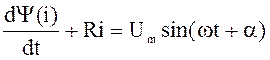

В правой части - функция времени; это - уравнение с неразделяющимися переменными. Следовательно, метод аналитической аппроксимации неприменим. Метод КЛА громоздок. Применимы метод условной линеаризации и численные методы интегрирования.

Выполним расчет переходного процесса методом условной линеаризации. В установившемся режиме  wL_э >>R, поэтому слагаемым  Ri  можно пренебречь.

Y_¥ »,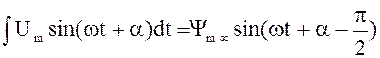

где 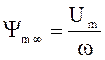, которому соответствует  I_m¥.

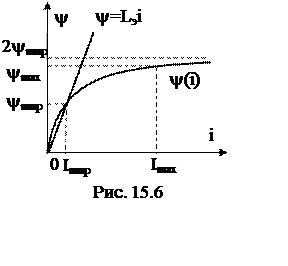
Через точку   (Y_m¥, I_m¥)  проводим прямую

Y= L_эi (рис. 15.6).

Здесь .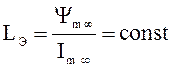

Уравнение становится линейным .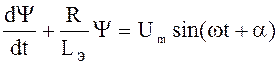

Его решение    ,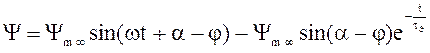

где .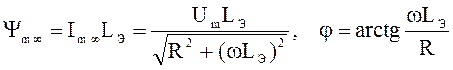

Обычно    wL_э >>R    и 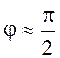   .    Тогда .

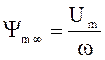Самый тяжелый переходный процесс при a=0.

.

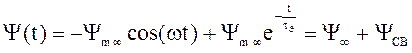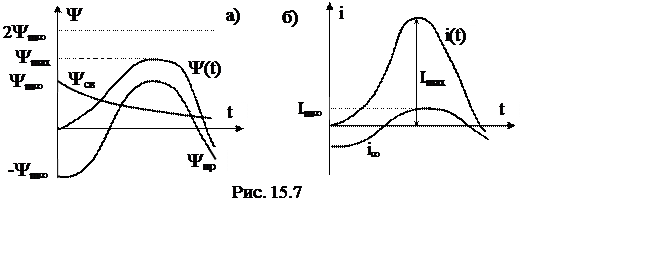
Графики    Y(t) и  i(t)  представлены на рис. 15.7а и б.

Таким образом, в первые моменты после включения катушки Y_max может достигать 2Y_m, а ток I_max  во много раз (20-50 раз) превышает амплитуду установившегося значения.

Например, в силовых трансформаторах значению Y_m¥ соответствует , а .

При В_max=2В_m¥=2,8 Тл;  I_max»50I_хх»2,5І_н. Такой всплеск тока может привести к срабатыванию максимальной токовой защиты при включении трансформатора.