Итерационный расчет
магнитной цепи состоит в многократном решении системы уравнений (5.1)–(5.3) в
направлении от стартовой величины к критериальной. Выбирается произвольное
значение стартовой функции (например, ![]() ),
решается система уравнений (5.1)–(5.3) и по выбранному значению индукции определяется
критериальная функция (например,
),
решается система уравнений (5.1)–(5.3) и по выбранному значению индукции определяется
критериальная функция (например, ![]() ). Найденное значение
критериальной функции сравнивается с заданной величиной и при несовпадении этих
значений расчет повторяется до их сходимости с требуемой точностью.
). Найденное значение
критериальной функции сравнивается с заданной величиной и при несовпадении этих
значений расчет повторяется до их сходимости с требуемой точностью.
Порядок действий следующий:
· Произвольно выбирается первое
приближение стартовой величины ![]() = 0,4 Тл.
= 0,4 Тл.
· По кривой намагничивания стали (табл.
5.3) для выбранного значения ![]() = 0,4 Тл определяется
соответствующее значение магнитной напряженности первого приближения в третьем
сердечнике магнитной цепи
= 0,4 Тл определяется
соответствующее значение магнитной напряженности первого приближения в третьем
сердечнике магнитной цепи ![]() = 59,7 А/м.
= 59,7 А/м.
· С учетом того что ![]() =
= ![]() ,
определяется первое приближение магнитной напряженности в немагнитном зазоре
,
определяется первое приближение магнитной напряженности в немагнитном зазоре
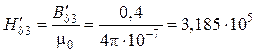 А/м.
А/м.
· Определяется магнитный поток первого
приближения в третьей ветви магнитной цепи ![]() =
= ![]() S3 = 0,4×6×10–3 = 2,4 мВб.
S3 = 0,4×6×10–3 = 2,4 мВб.
· Из уравнения (5.2) отыскивается
магнитная напряженность ![]() первого приближения во
втором сердечнике магнитопровода
первого приближения во
втором сердечнике магнитопровода
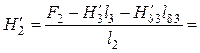
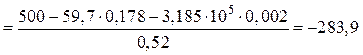 А/м.
А/м.
· По кривой намагничивания стали (табл.
5.3) для найденного значения ![]() определяется величина
индукции первого приближения во втором сердечнике магнитопровода
определяется величина
индукции первого приближения во втором сердечнике магнитопровода ![]() = – 1,0735 Тл.
= – 1,0735 Тл.
· Рассчитывается величина магнитного потока первого приближения во втором сердечнике
![]() =
= ![]() S2
= – 1,0735×6×10–3 = – 6,44 мВб.
S2
= – 1,0735×6×10–3 = – 6,44 мВб.
· Из уравнения (5.1) определяется магнитный поток первого приближения в первом сердечнике
![]() =
= ![]() –
– ![]() = 2,4 –
(– 6,44) = 8,84 мВб.
= 2,4 –
(– 6,44) = 8,84 мВб.
· Находится значение магнитной индукции первого приближения в первом сердечнике
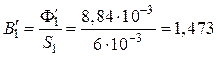 Тл.
Тл.
· Соответственно найденному значению
индукции ![]() по кривой намагничивания (табл. 5.3)
определяется первое приближение магнитной напряженности в первом сердечнике
по кривой намагничивания (табл. 5.3)
определяется первое приближение магнитной напряженности в первом сердечнике ![]() = 1697 А/м,
= 1697 А/м,
· Из уравнения (5.3) определяется первое приближение критериальной величины
![]() А.
А.
Рассчитанное значение
критериальной величины сравнивается с заданным значением этой функции (F1 = 1000 A) и при несовпадении
результатов повторяется расчет системы уравнений (5.1)–(5.3) при новом значении
(второе приближение) индукции (например, ![]() =
= 0,3 Тл). Полученное значение второго приближения критериальной величины
(например,
=
= 0,3 Тл). Полученное значение второго приближения критериальной величины
(например, ![]() ) вновь сравнивается с заданным значением.
При несовпадении величин расчет повторяется до тех пор, пока значение
критериальной величины очередного приближения не совпадет с требуемой точностью
с ее заданным значением. Данный метод наиболее эффективен при использовании
вычислительной техники. Однако если применить метод последовательного
приближения в сочетании с графическим методом, то по результатам трех
приближений можно определить истинное значение индукции в третьем сердечнике и
вслед за этим по приведенному выше алгоритму расчета системы уравнений
(5.1)–(5.3) найти истинные значения всех магнитных потоков в цепи. Для этого
достаточно по результатам трех приближений (см. табл. 5.4) построить характеристику
F1 = f(B1), представленную на рис. 5.3, и по ней определить
истинное значение индукции В1 для заданного значения МДС F1 = 1000 A.
) вновь сравнивается с заданным значением.
При несовпадении величин расчет повторяется до тех пор, пока значение
критериальной величины очередного приближения не совпадет с требуемой точностью
с ее заданным значением. Данный метод наиболее эффективен при использовании
вычислительной техники. Однако если применить метод последовательного
приближения в сочетании с графическим методом, то по результатам трех
приближений можно определить истинное значение индукции в третьем сердечнике и
вслед за этим по приведенному выше алгоритму расчета системы уравнений
(5.1)–(5.3) найти истинные значения всех магнитных потоков в цепи. Для этого
достаточно по результатам трех приближений (см. табл. 5.4) построить характеристику
F1 = f(B1), представленную на рис. 5.3, и по ней определить
истинное значение индукции В1 для заданного значения МДС F1 = 1000 A.
Т а б л и ц а 5.4
|
В3, Тл |
Н3, А/м |
Нd3 = В3/m0, А/м |
Ф3, мВб |
Н2, А/м |
В2, Тл |
Ф2, мВб |
Ф1, мВб |
В1, Тл |
Н1, А/м |
I1W1, А |
|
0,4 0,3 0,35 |
59,7 45 52,2 |
3,185×105 2,389×105 2,786×105 |
2,4 1,8, 2,1 |
–283,9 28,8 –126,5 |
–1,074 0,193 –0,792 |
–6,44 1,15 –4,75 |
8,84 0,65 6,85 |
1,473 1,083 1,142 |
1697 359 406 |
1529 724 776,8 |
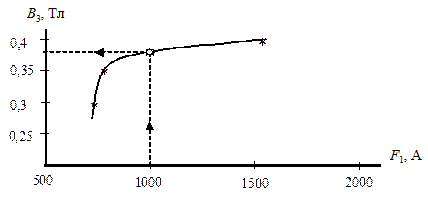
Рис. 5.3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.