Электротехника \ Теоретические основы электротехники

Определение магнитной индукции участков стального магнитопровода, страница 10

О к о н ч а н и е т а б л. 5.7

Номер варианта	Номер схемы	x_L, x_C	r₁	U_вх	Номер варианта	Номер схемы	x_L, x_C	r₁	U_вх
Номер варианта	Номер схемы	Ом	Ом	В	Номер варианта	Номер схемы	Ом	Ом	В
79	1	140	450	120	90	6	150	50	60
80	2	50	350	40	91	1	200	200	130
81	3	100	90	60	92	2	100	150	50
82	4	70	180	60	93	3	90	60	50
83	5	55	170	60	94	4	50	170	50
84	6	100	10	50	95	5	45	190	40
85	1	100	300	100	96	6	200	50	150
86	2	80	400	45	97	1	150	500	180
87	3	50	70	100	98	2	100	110	60
88	4	40	100	100	99	3	80	60	50
89	5	65	180	60	100	4	60	200	60

Указания к расчету

Для расчета схем, представленных на рис. 5.6–5.11, может быть использован метод последовательных приближений. Задавшись комплексом произвольной величины (тока или напряжения) в удаленной от источника ветви, с помощью законов Кирхгофа определяют комплексное напряжение на входе цепи. Полученное значение входного напряжения сравнивается с заданным и при несовпадении этих значений расчет повторяется до их сходимости с требуемой точностью.

Если известны вольт-амперные U_вх(I₁) и фазоамперные j₁(I₁) характеристики рассматриваемых схем, то заданное входное напряжение позволяет определить по этим характеристикам комплекс входного тока и вслед за этим с помощью законов Кирхгофа определить все остальные токи и напряжения в цепи.

В режиме резонанса входной ток должен быть в фазе с входным напряжением. Поэтому значение входного тока в режиме резонанса определяется по точке пересечения фазоамперной характеристики с осью абсцисс (т.е. при j₁ = 0). Найденное значение резонансного входного тока позволяет определить (с помощью законов Кирхгофа) напряжения и токи во всех участках цепи в том числе и в нелинейном элементе. Отношение 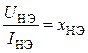характеризует величину сопротивления нелинейного элемента в режиме резонанса.

Подпись:
Рис. 5.12 Величина сопротивления нелинейного элемента в режиме резонанса может быть также найдена посредством определения комплексного входного сопротивления схемы . В режиме резонанса цепь должна быть активной, поэтому . Данное тождество, включающее в себя искомое сопротивление нелинейного элемента, позволяет его найти.

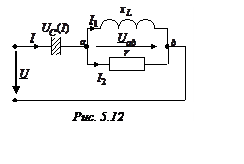
В качестве примера рассматривается цепь, представленная на рис. 5.12.

Схема состоит из линейных элементов r = 100 Ом; x_L = 80 Ом и нелинейного конденсатора, вольт-амперная характеристика которого для действующих значений напряжения и тока приведена в табл. 5.8.

Т а б л и ц а 5.8

U_C, В	10	20	30	40	50	60	70	80	90	100	110	120
I, А	0,4	0,7	0,9	1,0	1,08	1,14	1,18	1,21	1,24	1,28	1,3	1,34

Рассчитать токи в ветвях схемы при U = 60 В, пренебрегая несинусоидальностью режима. Определить действующее значение напряжения на входе цепи, при котором в цепи будет иметь место резонанс напряжений. Найти сопротивление нелинейного конденсатора в режиме резонанса.

Р е ш е н и е

1 2 3 4 5 6 7 8 9 10 11 12

Скачать файл