Исследование собственных колебаний струны. Измерения скорости поперечной волны теория исследуемого явления (Лабораторная работа № 12к)

ЛАБОРАТОРНАЯ РАБОТА №12к

ИССЛЕДОВАНИЕ СОБСТВЕННЫХ КОЛЕБАНИЙ СТРУНЫ.

ИЗМЕРЕНИЯ СКОРОСТИ ПОПЕРЕЧНОЙ ВОЛНЫ

ТЕОРИЯ ИССЛЕДУЕМОГО ЯВЛЕНИЯ

Если тело совершает колебания вследствие однократно приложен­ной силы без последующего воздействия на него, то колебания тела называется собственными (свободными).

Рассмотрим свободные поперечные колебания струны. Концы струны закреплены. Натяжение струны создается силой Р, направленной вдоль струны по оси X.  Если струну вывести из положения равновесия си­лой, много меньшей Р и направленной перпендикулярно оси X, то в струпе возникает поперечная волна, дифференциальное уравнение ко­торой имеет вид:

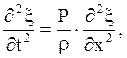                                                                        (1)

где x - смещение произвольной точки струны (x = x(t)).

 В уравнении (1)  

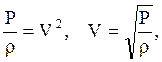                                                                 (2)

где Р - сила натяжения струны; r - линейная плотность струны (масса единица длины); V - скорость волны.

Колебания распространяется к закрепленным концам струны, от­ражаются и, встречаясь, накладываются. В результате интерференции образуется стоячая волна, амплитуда А которой является периоди­ческой функцией координаты X (рис.1). Точки с минимальной амп­литудой колебаний называется узлами, с максимальной - пучностями. Расстояние между соседними узлами (пучностями) равно половине дли­ны волны l/2. Так как на концах струны смещение x по условию равно нулю, то устойчивыми должны быть только колебания, при которых на длине струны укладывается целое число полудлин волн

                                                                                (3)

где n = 1, 2, 3 ...;  l - длина волны.

По определению длины волны

                                                   (4)

где Т - период;  u - частота. Из уравнений (2) - (4) имеем:

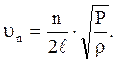                                                                    (5)

Из (5) следует, что при заданных  и Р струна характеризуется набором собственных частот, соответствующих n = 1, 2, 3 ... . Минимальная частота (n = 1) называется основной, остальные - обертонами. Наличие или отсутствие обертонов определяется услови­ями возбуждения. При изменении натяжения Р изменяется в соответст­вии с (5) и набор собственных частот.

При заданной частоте каждому из значений n при соответствующем натяжении Р должна отвечать своя длина волны и своя скорость волны V.

В соответствии с изложенным, при r = const следует ожидать

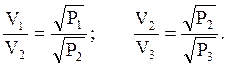                                                         (6)

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Постановка задачи

Задачей эксперимента является проверка соотношения (6). Для измерения предлагается метод резонанса.

Теория измерений

Амплитуда собственных колебаний струны, вызванных единичным воздействием, убывает во времени вследствие потерь энергии на тре­ние, сопротивление среды и т.д. Наблюдаемые колебания являются затухающими.

Колебания под действием периодического внешнего воздействия являются вынужденными и происходят с частотой внешнего воздействия. Амплитуда вынужденных колебаний зависит от соотношения частот вынуждающей силы u_В и собственной. Амплитуда будет максимальна при частоте u_В, близкой к одной из собственных частот струны, опре­деляемых выражением (5).

Задавая частоту u_В и добиваясь максимума амплитуды изменением силы натяжения Р при n = 1, 2, 3, можно измерить скорости (кос­венно) и проверить соотношение (6).

Принципиальная схема установки

Струна, помещенная между полюсами электромагнита, натягивается силой Р.  Р - сила натяжения струны (вес груза, подвешенного к струне длиной ), рис. 2. Через катушку электромагнита пропуска­ется переменный ток с частотой  u_В = 50 Гц, создающий переменное маг­нитное поле с индукцией В. По струне пропускается постоянный ток I = I.5¸2A. На элемент струны  действует внешняя периодичес­кая сила  (сила Ампера). Место приложения силы можно ме­нять путем перемещения электромагнита вдоль струны.

(В = B_oSin2pu_В. Здесь В₀ - амплитуда магнитной индукции).