Измерение отношения теплоемкости воздуха при постоянном давлении к его теплоемкости при постоянном объеме (Лабораторная работа № 8мс)

Лабораторная работа №8мс

ИЗМЕРЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТИ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ К ЕГО ТЕПЛОЕМКОСТИ ПРИ ПОСТОЯННОМ ОБЪЕМЕ

Постановка задачи

Задачей эксперимента является измерение отношения теплоёмкос­ти воздуха при постоянном давлении и его теплоёмкости при постоян­ном объёме.

Для измерения предлагается метод адиабатического расширения газа с последующей изохорической выдержкой.

Теория измерений и принципиальная схема установки

Теплоёмкостью называется физическая величина, численно рав­ная количеству теплоты, которое необходимо сообщить телу, чтобы повысить его температуру на один градус.

Теплоемкость единицы массы называется удельной теплоёмкостью, а теплоёмкость одного моля вещества – молярной теплоёмкостью.

Таким образом,

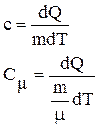
,                                                                  (1)

,                                                                  (2)

где с и С_m – удельная и молярная теплоёмкости; dQ – количество теплоты, необходимое для нагревания массы m на dТ градусов,  – молярная  масса вещества,  –  число молей.

Молярная и удельная теплоёмкости связаны соотношением

.

Теплоёмкость зависит от условия нагревания и температуры.

Рассмотрим теплоёмкости идеального газа при его изобарическом (Р=const) и изохорическом (V=const) нагревании. По первому началу термодинамики

dQ =dU+dA.                                                                              (3)

Если к системе энергия подводится, то dQ>0, отводится – dQ<0.

Если система совершает работу, то dA > 0 (и наоборот).

Если dU > 0, то внутренняя энергия возрастает (и наоборот).

Изменение внутренней энергии идеального газа

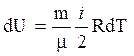,                                                                     (4)          

где i – число степеней свободы (число независимых координат, однозначно определяющих положение частицы в пространстве; для одноатомных молекул i = 2, для двухатомных i = 5, для многоатом­ных i = 6).

Для изобарического процесса:

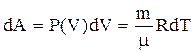,                                                         (5)          

Из уравнений (3) - (5) имеем:

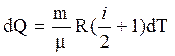.                                                              (6)

Для изохорического процесса dА = 0 и

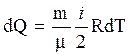.                                                                     (7)         

Из (2), (6) и (7) имеем:

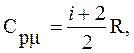                                                                       (8)

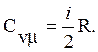                                                                              (9)

Отношение теплоёмкостей

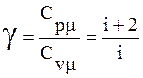.                                                                  (10)

Таким образом, теплоёмкость идеального газа не зависит от температуры (пока i не зависит от Т) и является  функцией процес­са.

Адиабатическим называется процесс, протекающий без теплооб­мена (dQ = 0).

Для этого процесса dU= - dA и

                                                               (11)

Из уравнения состояния идеального газа

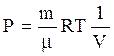.                                                                         (12)

Уравнение (11) с учётом (12) дает

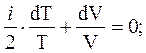
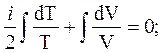                                   (13)

Из (10) находим 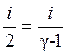. Тогда (13) принимает вид

                                                                     (14)

Для любого процесса при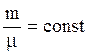

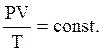                                                                           (15)

Из (14) и (15) имеем

                                                                            (16)

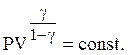                                                                      (17)

Уравнения (14), (16), (17) попарно связывают макроскопические параметры при адиабатическом процессе, по автору называются уравнениями Пуассона. 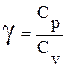 выступает показателем адиабаты.

Абсолютная теплоизоляция системы невозможна. В этом смысле адиабатический процесс является идеальным. Быстрые процессы можно считать адиабатическими.

Изотермический процесс тоже является идеальным, так как требует бесконечно большой скорости теплообмена или бесконечно малой скорости самого процесса. Для изотермического процесса PV = const , и показатель изотермы равен единице.

Все реальные процессы протекают с конечной скоростью, лежат между изотермическим и адиабатическим и называются политропическими. (æ- показатель политропы, 1æγ).

Показатель адиабаты, рассчитанный по формуле (10) через степени свободы, назовем теоретическим, а измеренный с использованием уравнений Пуассона – экспериментальным.

Пусть с некоторым количеством газа (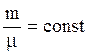), проведены процессы, представленные графически на рис. 1.

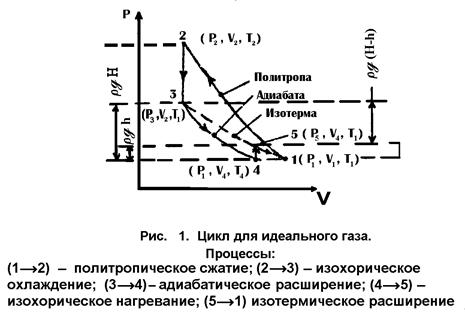
Для процесса  как адиабатического на основании (17)

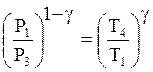.                                                               (18)

Для  изохорического процесса

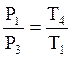.                                                                              (19)

Подставляем (19) и (18) и логарифмируем:

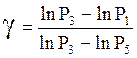.                                                                   (20)

Для малых разностей давлений из (20) имеем:

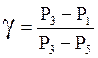.                                                                         (21)

При измерении разностей давлений жидкостным манометром

            P₃ – P₁ = H; P₃ – P₅ = rg(H – h),

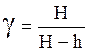                     ,                                                     (22)

где Н и h – разностей уровней жидкостей в коленах манометра; r– плотность жидкости; g – ускорение свободного падения.

Для эксперимента рекомендуется метод накачивания и выпуска воздуха с изохорическими выдержками после накачивания и выпуска. Рассмотрим метод подробнее.

Закачаем воздух в первоначально открытый сосуд объёма V₂ до давления Р₂ . Возможные варианты представим графиками рис. 2

Для накачивания:

; ;

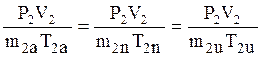      V_1a < V_1n < V_1u ; m_2a < m_2n <m_2u ;

                  T_2u > T_2n > T₁

                                                                                                               При изотермическом (очень медленном) накачивании повышение давления полностью обусловлено ростом концентрации молекул в сосуде.