Дифракция лазерного света на отверстии и диске (метод зон Френеля) (Лабораторная работа № 9лок)

Лабораторная работа 9 лок

ДИФРАКЦИЯ ЛАЗЕРНОГО СВЕТА НА ОТВЕРСТИИ И ДИСКЕ (МЕТОД ЗОН ФРЕНЕЛЯ)

Краткая теория

1. ПРИНЦИП ГЮЙГЕНСА — ФРЕНЕЛЯ

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифрак­ция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Явление сильно зависит от соотношения между длиной волны и размерами препятст­вий. Если длина волны сравнима с размерами препятствия, дифракция выражена очень сильно, если длина волны значительно меньше разме­ров препятствия - дифракция проявляется слабо и обнаруживается с трудом. Особенно это касается оптических явлений.

Явление дифракции волн можно понять, опираясь на принцип Гюйгенса. Однако этот принцип не дает никаких указаний об ампли­туде, а, следовательно, и об интенсивности волн (интенсивность про­порциональна квадрату амплитуды), распространяющихся в различ­ных направлениях. Этот недостаток был устранен Френелем, который дополнил принцип Гюйгенса представлением об интерференции вто­ричных волн.

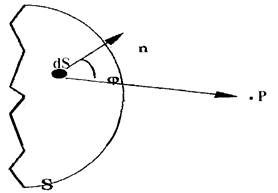
Рис.9.1.  Волновая поверхность

Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства.

Пусть S — волновая поверхность некоторого источника. Тогда амплитуда светового колебания в некоторой точке Р, лежащей за этой поверхностью, может быть, согласно Френелю, найдена из следую­щих соображений. Каждый элемент dS поверхности S является источ­ником вторичной сферической волны, амплитуда которой пропорцио­нальна величине этого элемента dS. Кроме того, амплитуда сфериче­ской волны убывает с расстоянием r от источника  по закону  и зависит от угла j между нормалью n к поверхности dS и направле­нием на точку наблюдения Р. Т.е. с увеличением угла и расстояния до точки Р амплитуда монотонно уменьшается. Нахождение результирующей ампли­туды от всей волновой поверхности S сводится к нахождению векторных сумм от отдельных элементов dS и представляет собой сложную задачу. Однако в случаях, отличающихся симметрией, нахож­дение амплитуды результирующего колебания значительно уп­рощается.

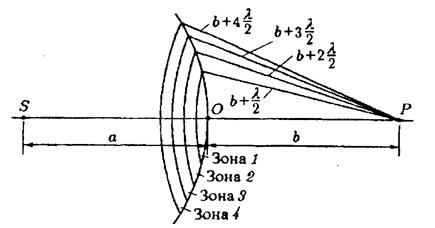
а — схема разбиения на зоны;

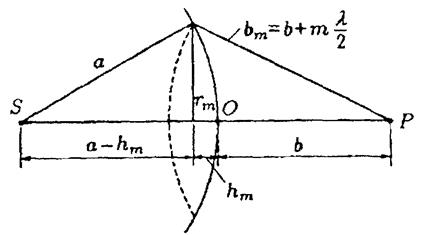
б - к расчету параметров зон Френеля.

Рис.9.2.  К методу зон Френеля

ЗОНЫ ФРЕНЕЛЯ

Применим принцип Гюйгенса - Френеля для нахождения ампли­туды светового колебания, возбуждаемого в точке Р сферической вол­ной, распространяющейся в однородной среде от точечного источ­ника S (рис.9.2). Волновая поверхность такой волны симмет­рична относительно прямой SP. Воспользовавшись этим, Френель раз­бил волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки Р отличаются на, где λ — длина волны в той среде в которой распространяется свет. Видно, что расстояние b_m от внешнего края m-й зоны до точки Р можно представить следующим образом:

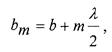(9.1)

где b - расстояние от вершины волновой поверхности O до точки Р.

Колебания, приходящие в точку Р от аналогичных точек двух со­седних зон будут находиться в противофазе. Поэтому и результи­рующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на π.

Для оценки амплитуд колебаний нужно найти площади зон, их расстояния до точки наблюдения Р и угол между нормалью к поверхно­сти зоны и направлением на точку Р. Из простых геометриче­ских вычислений, которые здесь опускаются, следует:

1. Площадь m-й зоны 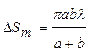не зависит от номера зоны и, следовательно, они примерно одинаковые (во всяком случае